
ЁОЬтФПЁПвбжЊЪ§жсЩЯСНЕуAЃЌBЖдгІЕФЪ§ЗжБ№ЪЧЉ10ЃЌ8ЃЌPЃЌQЃЌNЮЊЪ§жсЩЯШ§ИіЖЏЕуЃЌЕуPДгЕуAГіЗЂЫйЖШЮЊУПУы2ИіЕЅЮЛЃЌЕуQДгЕуBГіЗЂЃЌЫйЖШЮЊЕуPЕФ2БЖЃЌЕуNДгдЕуГіЗЂЃЌЫйЖШЮЊУПУы1ИіЕЅЮЛЃЎ
ЃЈ1ЃЉШєPЃЌQСНЕуВЛЖЏЃЌЖЏЕуNЪЧЯпЖЮABЕФШ§ЕШЗжЕуЪБЃЌЕуNЫљБэЪОЕФЪ§ЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєЕуPЯђзѓдЫЖЏЃЌЭЌЪБЕуQЯђгвдЫЖЏЃЌЧѓЖрГЄЪБМфЕуPгыЕуQЯрОр32ИіЕЅЮЛЃП
ЃЈ3ЃЉШєЕуPЃЌQЃЌNЭЌЪБЖМЯђгвдЫЖЏЧѓЖрГЄЪБМфЕуNЕНЕуPКЭЕуQЕФОрРыЯрЕШЃП
![]()
ЁОД№АИЁПЃЈ1ЃЉ2ЛђЉ4ЃЛЃЈ2ЃЉО![]() УыЕуPгыЕуQЯрОр32ИіЕЅЮЛЃЛЃЈ3ЃЉОЙ§0.5УыЕуNЕНPЃЌQСНЕуЕФОрРыЯрЕШ
УыЕуPгыЕуQЯрОр32ИіЕЅЮЛЃЛЃЈ3ЃЉОЙ§0.5УыЕуNЕНPЃЌQСНЕуЕФОрРыЯрЕШ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнAЁЂBЫљБэЪОЕФЪ§ПЩЕУABЃН18ЃЌдйгЩЖЏЕуNЪЧЯпЖЮABЕФШ§ЕШЗжЕуПЩЕУД№АИЃЛЃЈ2ЃЉЩшОЙ§tУыЕуPгыЕуQЯрОр32ИіЕЅЮЛЃЌгЩЬтвтЕУPЕФдЫЖЏОрРы+ABЕФГЄ+QЕФдЫЖЏОрРыЃН32ЃЌИљОнЕШСПЙиЯЕСаГіЗНГЬЃЌдйНтМДПЩЃЛЃЈ3ЃЉЩшОЙ§xУыЕуNЕНPЃЌQСНЕуЕФОрРыЯрЕШЃЌИљОнЬтвтПЩЕУЕШСПЙиЯЕЃКPЁЂNЕФОрРыЃНNЁЂQЕФОрРыЃЌИљОнЕШСПЙиЯЕСаГіЗНГЬЃЌдйНтМДПЩЃЎ
НтЃКЃЈ1ЃЉЁпAЃЌBЖдгІЕФЪ§ЗжБ№ЪЧЉ10ЃЌ8ЃЌ
ЁрABЃН18ЃЌ
ЁпЖЏЕуNЪЧЯпЖЮABЕФШ§ЕШЗжЕуЃЌ
ЁрNЕуБэЪОЕФЪ§ЮЊ2ЛђЉ4ЃЌ
ЙЪД№АИЮЊЃК2ЛђЉ4ЃЛ
ЃЈ2ЃЉЩшОЙ§tУыЕуPгыЕуQЯрОр32ИіЕЅЮЛЃЌгЩЬтвтЕУЃК
2t+18+4tЃН32ЃЌ
НтЕУЃЌtЃН![]() ЃЌ
ЃЌ
Д№ЃКЩшО![]() УыЕуPгыЕуQЯрОр32ИіЕЅЮЛЃЛ
УыЕуPгыЕуQЯрОр32ИіЕЅЮЛЃЛ
ЃЈ3ЃЉЩшОЙ§xУыЕуNЕНPЃЌQСНЕуЕФОрРыЯрЕШЃЌгЩЬтвтЕУЃК
10Љ2x+xЃН8Љx+4xЃЌ
НтЕУЃЌxЃН0.5ЃЌ
Д№ЃКОЙ§0.5УыЕуNЕНPЃЌQСНЕуЕФОрРыЯрЕШЃЎ


 100ЗжДГЙиЦкФЉГхДЬЯЕСаД№АИ
100ЗжДГЙиЦкФЉГхДЬЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
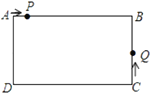
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌAB=4ЃЌЕуEдкЖдНЧЯпACЩЯЃЌСЌНгBEЁЂDEЃЌ
ЃЈ1ЃЉШчЭМ1ЃЌзїEMЁЭABНЛABгкЕуMЃЌЕБAE=![]() ЪБЃЌЧѓBEЕФГЄЃЛ
ЪБЃЌЧѓBEЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌзїEGЁЭBEНЛCDгкЕуGЃЌЧѓжЄЃКBE=EGЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌзїEFЁЭBCНЛBCгкЕуFЃЌЩшBF=xЃЌЁїBEFЕФУцЛ§ЮЊyЃЎЕБxШЁКЮжЕЪБЃЌyШЁЕУзюДѓжЕЃЌзюДѓжЕЪЧЖрЩйЃПЕБЁїBEFЕФУцЛ§ШЁЕУзюДѓжЕЪБЃЌдкжБЯпEFШЁЕуPЃЌСЌНгBPЁЂPCЃЌЪЙЕУЁЯBPC=45ЁуЃЌЧѓEPЕФГЄЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїЦяздааГЕШЅбЇаЃЃЌзюГѕвдФГвЛЫйЖШдШЫйааЪЛЃЌжаЭОздааГЕЗЂЩњЙЪеЯЃЌЭЃЯТРДаоГЕЕЂЮѓСЫМИЗжжгЃЌЮЊСЫАДЪБЕНаЃЃЌЫћМгПьСЫЫйЖШЃЌШдБЃГждШЫйааЪЛЃЌНсЙћзМЪБЕНаЃЃЌЕНаЃКѓЃЌаЁУїЛСЫздааГЕааНјТЗГЬs(km)гыааНјЪБМфt(h)ЕФЭМЯѓЃЌШчЭМЫљЪОЃЌЧыЛиД№ЃК
(1)етИіЭМЯѓЗДгГСЫФФСНИіБфСПжЎМфЕФЙиЯЕЃП
(2)ИљОнЭМЯѓЬюБэЃК
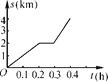
ЪБМфt/h | 0 | 0.2 | 0.3 | 0.4 |
ТЗГЬs/km |
(3)ТЗГЬsПЩвдПДГЩЪБМфtЕФКЏЪ§Т№ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
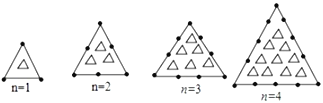
ЁОЬтФПЁПЙлВьЯТСаЭМаЮЙцТЩЃКЕБ![]() ЪБЃЌЭМаЮЁАЁББШЁАЁїЁБЕФИіЪ§Щй______Иі.
ЪБЃЌЭМаЮЁАЁББШЁАЁїЁБЕФИіЪ§Щй______Иі.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНаЮ![]() жаЃЌ
жаЃЌ![]() РхУзЃЌ
РхУзЃЌ![]() РхУз.ЖЏЕу
РхУз.ЖЏЕу![]() Дг
Дг![]() ГіЗЂЃЌвд2РхУз/УыЕФЫйЖШби
ГіЗЂЃЌвд2РхУз/УыЕФЫйЖШби![]() дЫЖЏЃЌЕН
дЫЖЏЃЌЕН![]() ЕуЭЃжЙдЫЖЏЃЛЭЌЪБЕу
ЕуЭЃжЙдЫЖЏЃЛЭЌЪБЕу![]() Дг
Дг![]() ЕуГіЗЂЃЌвд4РхУз/УыЕФЫйЖШби
ЕуГіЗЂЃЌвд4РхУз/УыЕФЫйЖШби![]() дЫЖЏЃЌЕН
дЫЖЏЃЌЕН![]() ЕуЭЃжЙдЫЖЏ.Щш
ЕуЭЃжЙдЫЖЏ.Щш![]() ЕудЫЖЏЕФЪБМфЮЊ
ЕудЫЖЏЕФЪБМфЮЊ![]() УыЃЈ
УыЃЈ![]() ЃЉ.
ЃЉ.
ЃЈ1ЃЉЕу![]() дк
дк![]() ЩЯдЫЖЏЪБЃЌ
ЩЯдЫЖЏЪБЃЌ![]() ______ЃЌ
______ЃЌ![]() ______ЃЈгУКЌ
______ЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЛЕу
ЕФДњЪ§ЪНБэЪОЃЉЃЛЕу![]() дк
дк![]() ЩЯдЫЖЏЪБЃЌ
ЩЯдЫЖЏЪБЃЌ![]() ______ЃЌ
______ЃЌ![]() ______ЃЛЃЈгУКЌ
______ЃЛЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉ
ЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉЕБ![]() ЮЊКЮжЕЃЌ
ЮЊКЮжЕЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЁЂ
ЁЂ![]() СНЕудкдЫЖЏТЗЯпЩЯЯрОрЕФТЗГЬЮЊ4РхУзЃЛ
СНЕудкдЫЖЏТЗЯпЩЯЯрОрЕФТЗГЬЮЊ4РхУзЃЛ
ЃЈ4ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕчЦїГЌЪаЯњЪлAЁЂBСНжжВЛЭЌаЭКХЕФЕчЗчЩШЃЌУПжжаЭКХЕчЗчЩШЕФЙКТђЕЅМлЗжБ№ЮЊУПЬЈ310дЊЃЌ460дЊЃЎ
ЃЈ1ЃЉШєФГЕЅЮЛЙКТђAЃЌBСНжжаЭКХЕФЕчЗчЩШЙВ50ЬЈЃЌЧвЧЁКУжЇГі20000дЊЃЌЧѓAЃЌBСНжжаЭКХЕчЗчЩШИїЙКТђЖрЩйЬЈЃП
ЃЈ2ЃЉШєЙКТђAЃЌBСНжжаЭКХЕФЕчЗчЩШЙВ50ЬЈЃЌЧвжЇГіВЛГЌЙ§18000дЊЃЌЧѓAжжаЭКХЕчЗчЩШжСЩйвЊЙКТђЖрЩйЬЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃбЇЩњРћгУЫЋанЪБМфШЅОрбЇаЃ10 kmЕФЬьЦНЩНЩчЛсЪЕМљЛюЖЏЃЌвЛВПЗжбЇЩњЦяЕчЦПГЕЯШзпЃЌЙ§СЫ20 minКѓЃЌЦфгрбЇЩњГЫЙЋНЛГЕбиЯрЭЌТЗЯпГіЗЂЃЌНсЙћЫћУЧЭЌЪБЕНДяЃЎвбжЊЙЋНЛГЕЕФЫйЖШЪЧЕчЦПГЕбЇЩњЫйЖШЕФ2БЖЃЌЧѓЦяЕчЦПГЕбЇЩњЕФЫйЖШКЭЙЋНЛГЕЕФЫйЖШЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
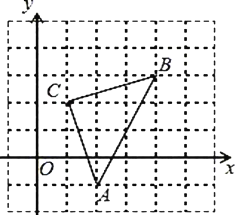
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌЁїABCЕФЖЅЕуЖМдкЭјИёЕуЩЯЃЌЦфжаЃЌCЕузјБъЮЊЃЈ1ЃЌ2ЃЉ.
ЃЈ1ЃЉаДГіЕуAЁЂBЕФзјБъЃКAЁЁ ЁЁЃЌBЁЁ ЁЁ ЃЛ
ЃЈ2ЃЉНЋЁїABCЯШЯђзѓЦНвЦ2ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНЁїA1B1C1ЃЌЛГіЁїA1B1C1ЃЛ
ЃЈ3ЃЉШєABБпЩЯгавЛЕуMЃЈaЃЌbЃЉЃЌЦНвЦКѓЖдгІЕФЕуM1ЕФзјБъЮЊ________________ЃЛ
ЃЈ4ЃЉЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯпЖЮABЃН4.8cmЃЌCЪЧЯпЖЮABЕФжаЕуЃЌDЪЧЯпЖЮCBЕФжаЕуЃЌЕуEдкABЩЯЃЌЧвCEЃН![]() ACЃЌдђDEЕФГЄЮЊ_____ЃЎ
ACЃЌдђDEЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com