
【题目】如图,已知点![]() ,点
,点![]() 是直线上的两点,
是直线上的两点,![]() 厘米,点
厘米,点![]() ,点
,点![]() 是直线上的两个动点,点
是直线上的两个动点,点![]() 的速度为1厘米/秒,点
的速度为1厘米/秒,点![]() 的速度为2厘米/秒.点
的速度为2厘米/秒.点![]() 分别从点
分别从点![]() ,点
,点![]() 同时相向出发沿直线运动
同时相向出发沿直线运动![]() 秒:
秒:
(1)求![]() 两点刚好重合时的
两点刚好重合时的![]() 值;
值;
(2)当![]() 两点重合后继续沿原来方向前进,求相距6厘米时的
两点重合后继续沿原来方向前进,求相距6厘米时的![]() 值;
值;
(3)当点![]() 离
离![]() 点的距离为2厘米时,求点
点的距离为2厘米时,求点![]() 离
离![]() 点的距离.
点的距离.

【答案】(1)4秒;(2)6秒;(3)7厘米或者5厘米
【解析】
(1)根据题意,两点重合,即相遇,列出等式,即可求解;
(2)根据其速度和相距距离或者路程除以速度列出等式即可;
(3)分两种情况求解:点Q在A点的右边和点Q在A点的左边,即可得解.
(1)因为运动时间为t秒.
由题意,得:t+2t=12,
解得t=4(秒);
(2)因为运动时间为t秒.
![]()
方法一:2(t-4)+(t-4)=6
3t-12=6
t=6(秒)
方法二:t=(12+6)÷(2+1)
t=6(秒)
(3)当点Q离A点的距离为2厘米时,分两种情况:
①点Q在A点的右边,如图所示:
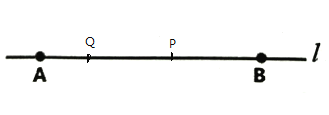
因为AB=12cm
此时,t=(12-2) ÷2=5,
P点经过了5厘米,点P离B点的距离为7厘米;
②点Q在A点的左边,如图所示:
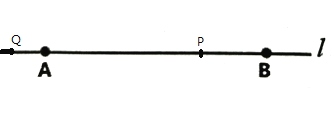
因为点Q运动了(12+2)÷2=7(秒)
此时,t=7,P点经过了7厘米,
所以点P离B点的距离为12-7=5(厘米).
综上所说,点P离B点的距离为7厘米或者5厘米.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
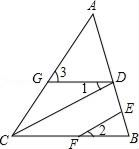
【题目】如图,已知,CD∥EF,∠1=∠2,求证:∠3=∠ACB.请补全证明过程.
证明:∵CD∥EF,( )
∴∠2=∠DCB,(两直线平行,同位角相等)
∵∠1=∠2,( )
∴∠1=∠DCB,( )
∴GD∥CB,( )
∴∠3=∠ACB,( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多边形上或内部的一点与多边形各顶点的连线,可以将多边形分割成若干个小三角形.如图,给出了四边形的三种具体分割方法,分别将四边形分割成了2个、3个、4个小三角形,这样我们就可以借助研究三角形的经验研究四边形了.
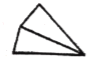
图①被分割成2个小三角形

图②被分割成3个小三角形

图③被分割成4个小三角形
(1)请按照上述三种方法分别将图中的六边形进行分割,并写出每种方法所得到的小三角形的个数:
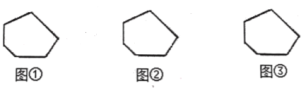
图①被分割成 个小三角形、图②被分割成 个小三角形、图③被分割成 个小三角形;
(2)如果按照上述三种分割方法分别分割![]() 边形,请写出每种方法所得到的小三角形的个数(用含
边形,请写出每种方法所得到的小三角形的个数(用含![]() 的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,
的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,![]() 边形分别可以被分割成 、 、 个小三角形.
边形分别可以被分割成 、 、 个小三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列![]() 个生产、生活现象中,可用“两点之间线段最短”来解释的是( )
个生产、生活现象中,可用“两点之间线段最短”来解释的是( )
A.用两根钉子就可以把木条固定在墙上
B.植树时,只要选出两棵树的位置,就能确定同一行树所在的直线
C.把弯曲的公路改直,就能缩短路程
D.砌墙时,经常在两个墙角的位置分别插一根木桩拉一条直的参照线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD,延长AB到E使BE=AB,连接BD,ED,EC,若ED=AD.
(1)求证:四边形BECD是矩形;
(2)连接AC,若AD=4,CD= 2,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴表示的是5个城市的国际标准时间(单位:时),如果北京的时间是2020年1月9日上午9时,下列说法正确的是( )

A.伦敦的时间是2020年1月9日凌晨1时
B.纽约的时间是2020年1月9日晚上20时
C.多伦多的时间是2020年1月8日晚上19时
D.汉城的时间是2020年1月9日上午8时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com