
����Ŀ����ͼ��1����AB=7cm��AC��AB��BD��AB ����ֱ�Ϊ A��B��AC=5cm����P ���߶� AB ���� 2cm/s ���ٶ��ɵ� A ���B �˶���ͬʱ���� Q ������ BD ���˶��������� ����ʱ��Ϊ t��s�������� P �˶�����ʱ���� Q �˶���֮��������
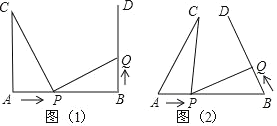
��1������ Q ���˶��ٶ���� P ���˶��ٶ���ȣ��� t=1 ʱ����ACP ����BPQ �Ƿ�ȫ�ȣ� ���жϴ�ʱ�߶� PC ���߶� PQ ��λ�ù�ϵ����ֱ�˵�����ɣ�
��2����ͼ��2��������AC��AB��BD��AB�� ��Ϊ ����CAB=��DBA=60�㡱���� Q ���˶��� ��Ϊ x cm/s�������������䣬���� P��Q �˶���ij��ʱ������ACP ����BPQ ȫ�ȣ������Ӧ�� x��t ��ֵ��
���𰸡���1����ACP�ա�BPQ��PC��PQ�����ɼ���������2��t=1s��x=2cm/s��t=![]() s��x=
s��x=![]() cm/s��
cm/s��
��������
��1������SAS֤�á�ACP�ա�BPQ���ó���ACP=��BPQ�����ɵó���APC+��BPQ=��APC+��ACP=90�������ɵó����ۣ�
��2���ɡ�ACP�ա�BPQ���������������AC=BP��AP=BQ����AC=BQ��AP=BP��������������ô𰸼��ɣ�
�⣺��1����ACP�ա�BPQ��PC��PQ��
�������£���t=1ʱ��AP=BQ=2��
��BP=7-2=5��
��BP=AC��
��AC��AB��BD��AB
���A=��B=90��
�ڡ�ACP�͡�BPQ�У�
 ��
��
���ACP�ա�BPQ��
���ACP=��BPQ��
���APC+��BPQ=��APC+��ACP=90����
���CPQ=90����
��PC��PQ��
��2��������ACP�ա�BPQ��
��AC=BP��AP=BQ���ɵã�5=7-2t��2t=xt
��ã�x=2��t=1��
������ACP�ա�BQP��
��AC=BQ��AP=BP���ɵã�5=xt��2t=7-2t
��ã�t=![]() �� x=5��
�� x=5��![]() =
=![]() ��
��
�ʵ�t=1s��x=2cm/s��t=![]() s��x=
s��x=![]() cm/sʱ����ACP���BPQȫ�ȣ�
cm/sʱ����ACP���BPQȫ�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A����2��3����B��4��3����C����1����3����
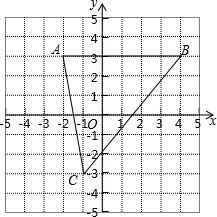
��1�����C��x��ľ��룻
��2���ֱ�����ABC�����߳���
��3����P��y���ϣ�����ABP�����Ϊ6ʱ����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������OAB�У���AOB=110�㣬�뾶OA=18��������OAB�ع���B��ֱ���۵�����Oǡ�����ڻ�AB�ϵĵ�D�����ۺ۽�OA�ڵ�C����AD�ij�Ϊ��������
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ڼ䣬ij����Ϸ�����С�ӭ���ˡ������һ����Ϸ�Ĺ����ǣ���һ��װ��![]() ����������ɸ�����ÿ�������ɫ��������ͬ���Ĵ��У������һ��������һ������͵õ�һ�����˸�����ߣ���֪�μ�������Ϸ�Ϊ
����������ɸ�����ÿ�������ɫ��������ͬ���Ĵ��У������һ��������һ������͵õ�һ�����˸�����ߣ���֪�μ�������Ϸ�Ϊ![]() �˴Σ�����Ϸ�����ŵĸ������Ϊ
�˴Σ�����Ϸ�����ŵĸ������Ϊ![]() ����
����
![]() ��μ�һ��������Ϸ��õ�������ߵĸ��ʣ�
��μ�һ��������Ϸ��õ�������ߵĸ��ʣ�
![]() ������ƴ��а���ӽ����ٸ���
������ƴ��а���ӽ����ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��A1��A2��A3������ͬһֱ���ϣ�AB��A1B��A1B1��A1A2��A2B2��A2A3��A3B3��A3A4����������B�Ķ���Ϊ![]() �����A2019A2020B2019�Ķ���Ϊ_______��
�����A2019A2020B2019�Ķ���Ϊ_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
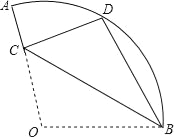
����Ŀ����ͼ������ABC�У���ACB=90����CD�����ߣ�AC=BC��һ���Ե�DΪ�����45�����Ƶ�D��ת��ʹ�ǵ����߷ֱ���AC��BC���ӳ����ཻ������ֱ�Ϊ��E��F��DF��AC���ڵ�M��DE��BC���ڵ�N��

��1����ͼ1����CE=CF����֤��DE=DF��
��2����ͼ2������EDF�Ƶ�D��ת�Ĺ����У�
��̽�������߶�AB��CE��CF֮���������ϵ����˵�����ɣ�
����CE=4��CF=2����DN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��3��0����B��0����1��������AB������B�Ĵ���BC��ʹBC��BA�����C������_____��
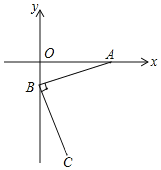
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��ͼ����ͼ��ʾ���Գ�����ֱ��
��ͼ����ͼ��ʾ���Գ�����ֱ��![]() �������½��ۣ���
�������½��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ�Ľ��۵ĸ�����( )
��������ȷ�Ľ��۵ĸ�����( )
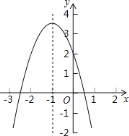
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��3��m����B����2����3����ֱ��AB��ij������������ͼ����������㣮
��1����ֱ��AB�ͷ����������Ľ���ʽ��
��2���۲�ͼ��ֱ��д����x����ʲô��Χʱ��ֱ��AB��˫���ߵ��·���
��3��������������ͼ�����Ƿ���ڵ�C��ʹ����OBC�����������OAB���������������ڣ�˵�����ɣ�������ڣ�����������������е�C�����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com