
【题目】已知:线段![]() .
.

(1)如图1,点![]() 沿线段
沿线段![]() 自点
自点![]() 向
向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,同时点
秒运动,同时点![]() 沿线段
沿线段![]() 自点
自点![]() 向
向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,经过_________秒,
秒运动,经过_________秒,![]() 、
、![]() 两点相遇.
两点相遇.
(2)如图1,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,点
秒运动,点![]() 出发
出发![]() 秒后,点
秒后,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,问再经过几秒后
秒运动,问再经过几秒后![]() 、
、![]() 相距
相距![]() ?
?
(3)如图2:![]() ,
,![]() ,
,![]() ,点
,点![]() 绕着点
绕着点![]() 以
以![]() 度
度![]() 秒的速度逆时针旋转一周停止,同时点
秒的速度逆时针旋转一周停止,同时点![]() 沿直线
沿直线![]() 自
自![]() 点向
点向![]() 点运动,假若点
点运动,假若点![]() 、
、![]() 两点能相遇,直接写出点
两点能相遇,直接写出点![]() 运动的速度.
运动的速度.
【答案】(1)5;(2)3秒或5秒;(3)14cm或4.8cm.
【解析】
(1)根据点P、Q运动路程和等于AB求解;
(2)分点P与点Q在相遇前与相遇后相距6cm两种情况列方程来解答;
(3)分P、Q在点O左右两边相遇来解答.
(1)30÷(2+4)=5(秒),
故答案为5;
(2)设再经过x秒后点P、Q两点相距6cm.
当点P在点Q左边时,2(x+3)+4x+6=30
解得x=3;
当点P在点Q右边时,2(x+3)+4x-6=30
解得x=5,
所以再经过3或5秒后点P、Q两点相距6cm;
(3)设点Q运动的速度为每秒xcm.
当P、Q两点在点O左边相遇时,[(180-60)÷60]x=30-2,
解得x=14;
当P、Q两点在点O右边相遇时,[(360-60)÷60]x=30-6,
解得x=4.8,
所以若P、Q两点能相遇点Q运动的速度为每秒14cm或4.8cm.


科目:初中数学 来源: 题型:
【题目】已知:线段![]() .
.
(1)如图1,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 秒运动,同时点
秒运动,同时点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 秒运动.
秒运动.
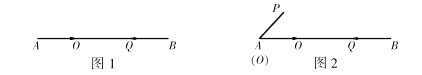
①问经过几秒后![]() 相遇?
相遇?
②几秒钟后![]() 相距
相距![]() ?
?
(2)如图2,![]() ,
,![]() ,点
,点![]() 以每秒
以每秒![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点运动,点
点运动,点![]() 自
自![]() 点向
点向![]() 点运动的同时线段
点运动的同时线段![]() 以每秒
以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转一周停止,假如
顺时针旋转一周停止,假如![]() 两点能相遇,求点
两点能相遇,求点![]() 运动的速度.
运动的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线L与y=2x+1的交于点A(2,a),与直线y=x+2的交于点B(b,1)
(1)求a,b的值;
(2)求直线l的函数表达式;
(3)求直线L、x轴、直线y=2x+1围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC ∠ACB ,BD 、CD 分别平分△ABC 的内角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延长线于点 E ,以下结论:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
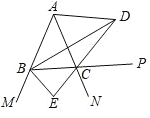
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用棋子摆成一组“上”字:

如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第![]() 个、第
个、第![]() 个图形中的“上”字分别需要用多少枚棋子?
个图形中的“上”字分别需要用多少枚棋子?
(2)第![]() 个图形中的“上”字需要用多少枚棋子?
个图形中的“上”字需要用多少枚棋子?
(3)七(3)班有![]() 名同学,能否让这
名同学,能否让这![]() 名同学按照以上规律恰好站成一个“上”字?若能,请计算最下面一“横”的学生数;若不能,请说明理由.
名同学按照以上规律恰好站成一个“上”字?若能,请计算最下面一“横”的学生数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为1,![]() ,
,![]() ,则有下列结论:①
,则有下列结论:①![]() ;②点C到EF的距离是2-1;③
;②点C到EF的距离是2-1;③![]() 的周长为2;④
的周长为2;④![]() ,其中正确的结论有( )
,其中正确的结论有( )
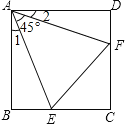
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位,元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列正确结论的序号是____.

①第24天的销售量为200件;
②第10天销售一件产品的利润是15元;
③第12天与第30天这两天的日销售利润相等;
④第30天的日销售利润是750元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
(1)若∠MON=60°,则∠ACG= °;若∠MON=90°,则∠ACG= °;
(2)若∠MON=n°,请求出∠ACG的度数;(用含n的代数式表示)
(3)如图2,若∠MON=n°,过C作直线与AB交于F,若CF∥OA时,求∠BGO-∠ACF的度数.(用含n的代数式表示).
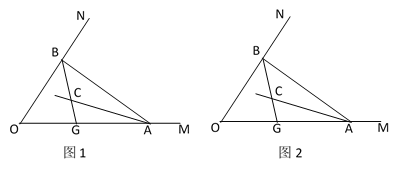
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com