
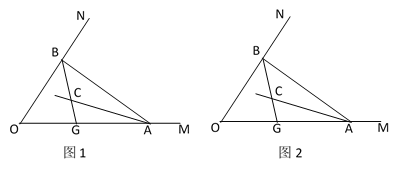
【题目】如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
(1)若∠MON=60°,则∠ACG= °;若∠MON=90°,则∠ACG= °;
(2)若∠MON=n°,请求出∠ACG的度数;(用含n的代数式表示)
(3)如图2,若∠MON=n°,过C作直线与AB交于F,若CF∥OA时,求∠BGO-∠ACF的度数.(用含n的代数式表示).
【答案】(1)60°;45°;(2)90°-![]() n;(3)90°-
n;(3)90°-![]() n.
n.
【解析】
(1)根据三角形的内角和求出∠ABO+∠BAO的度数,再根据角平分线的定义及外角的性质即可得到∠ACG的度数;
(2)根据(1)中的结论即可求出答案;
(3)根据角平分线的性质,平行线的性质得到∠ACF=∠CAO=∠BAC,利用外角的性质得到∠BGO-∠ACF=∠ACG,由此得到答案.
(1)∵∠MON+∠ABO+∠BAO=180°,
∴∠ABO+∠BAO=180°-∠MON,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠ABC=![]() ∠ABO,∠BAC=
∠ABO,∠BAC=![]() ∠BAO,
∠BAO,
当∠MON=60°,
∠ACG=∠ABC+∠BAC=![]() (∠ABO+∠BAO)=
(∠ABO+∠BAO)=![]() (180°-∠MON)=60°,
(180°-∠MON)=60°,
当∠MON=90°,
∠ACG=∠ABC+∠BAC=![]() (∠ABO+∠BAO)=
(∠ABO+∠BAO)=![]() (180°-∠MON)=45°,
(180°-∠MON)=45°,
故答案为:60°,45°;
(2)由(1)知∠ACG=![]() (180°-∠MON),
(180°-∠MON),
∵∠MON=n°,
∴∠ACG=![]() (180°-∠MON)=90°-
(180°-∠MON)=90°-![]() n;
n;
(3)∵AC平分∠BAO,
∴∠BAC=∠CAO
∵CF∥OA,
∴∠ACF=∠CAO=∠BAC,
∵∠BGO=∠ABG+∠BAO=∠ABG+2∠ACF,
∴∠BGO-∠ACF=∠ABG+2∠ACF-∠ACF=∠ABG+∠ACF=∠ABG+∠BAC=∠ACG,
∵∠MON=n°时∠ACG=90°-![]() n,
n,
∴∠BGO-∠ACF=90°-![]() n.
n.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】已知:线段![]() .
.

(1)如图1,点![]() 沿线段
沿线段![]() 自点
自点![]() 向
向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,同时点
秒运动,同时点![]() 沿线段
沿线段![]() 自点
自点![]() 向
向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,经过_________秒,
秒运动,经过_________秒,![]() 、
、![]() 两点相遇.
两点相遇.
(2)如图1,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,点
秒运动,点![]() 出发
出发![]() 秒后,点
秒后,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 厘米
厘米![]() 秒运动,问再经过几秒后
秒运动,问再经过几秒后![]() 、
、![]() 相距
相距![]() ?
?
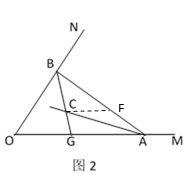
(3)如图2:![]() ,
,![]() ,
,![]() ,点
,点![]() 绕着点
绕着点![]() 以
以![]() 度
度![]() 秒的速度逆时针旋转一周停止,同时点
秒的速度逆时针旋转一周停止,同时点![]() 沿直线
沿直线![]() 自
自![]() 点向
点向![]() 点运动,假若点
点运动,假若点![]() 、
、![]() 两点能相遇,直接写出点
两点能相遇,直接写出点![]() 运动的速度.
运动的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
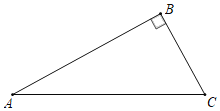
【题目】已知,如图,在直角三角形ABC中,∠ABC=90°,AC=10,BC=6,AB=8.P是线段AC上的一个动点,当点P从点C向点A运动时,运动到点A停止,设PC=x,△ABP的面积为y.求y与x之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要举办一次演讲比赛,每班只能选一人参加比赛.但八年级一班共有甲、乙两人的演讲水平相不相上下,现要在他们两人中选一人去参加全校的演讲比赛,经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛(胜者参赛).
游戏规则如下:在两个不透明的盒子中,一个盒子里放着两个红球,一个白球;另一个盒子里放着三个白球,一个红球,从两个盒子中各摸一个球,若摸得的两个球都是红球,甲胜;摸得的两个球都是白球,乙胜,否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
根据上述规则回答下列问题:
(1)从两个盒子各摸出一个球,一个球为白球,一个球为红球的概率是多少?
(2)该游戏公平吗?请用列表或树状图等方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活中,有人喜欢把传送的便条折成“ ”形状,折叠过程按图
”形状,折叠过程按图![]() 的顺序进行(其中阴影部分表示纸条的反面):
的顺序进行(其中阴影部分表示纸条的反面):

如果由信纸折成的长方形纸条(图①)长![]() 厘米,分别回答下列问题:
厘米,分别回答下列问题:
(1)如图①、图②,如果长方形纸条的宽为![]() 厘米,并且开始折叠时
厘米,并且开始折叠时![]() 厘米,那么在图②中,
厘米,那么在图②中,![]() ____厘米.
____厘米.
(2)如图②,如果长方形纸条的宽为![]() 厘米,现在不但要折成图②的形状,还希望纸条两端超出点
厘米,现在不但要折成图②的形状,还希望纸条两端超出点![]() 的部分
的部分![]() 和
和![]() 相等,使图②. 是轴对称图形,
相等,使图②. 是轴对称图形,![]() ______厘米.
______厘米.
(3)如图④,如果长方形纸条的宽为![]() 厘米,希望纸条两端超出点
厘米,希望纸条两端超出点![]() 的部分
的部分![]() 和
和![]() 相等,即最终图形是轴对称图形,试求在开始折叠时起点
相等,即最终图形是轴对称图形,试求在开始折叠时起点![]() 与点
与点![]() 的距离(结果用
的距离(结果用![]() 表示) .
表示) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com