
【题目】(1)观察思考:如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;
(2)模型构建:如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;
(3)拓展应用:某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握多少次手?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
![]()
【答案】(1)6条线段;(2)![]() ;(3)990次.
;(3)990次.
【解析】试题分析:(1)从左向右依次固定一个端点A、C、D找出线段,最后求和即可;(2)根据数线段的特点列出式子化简即可;(3)将实际问题转化成(2)的模型,借助(2)的结论即可得出结论.
试题解析:
(1)∵以点A为左端点向右的线段有:线段AB、AC、AD,
以点C为左端点向右的线段有线段CD、CB,
以点D为左端点的线段有线段DB,
∴共有3+2+1=6条线段;
(2)设线段上有m个点,该线段上共有线段x条,
则x=(m﹣1)+(m﹣2)+(m﹣3)+…+3+2+1,
∴x=![]() m(m﹣1);
m(m﹣1);
(3)把45位同学看作直线上的45个点,每两位同学之间的一握手看作为一条线段,
直线上45个点所构成的线段条数就等于握手的次数,
因此一共要进行![]() ×45×(45﹣1)=990次握手.
×45×(45﹣1)=990次握手.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是 . 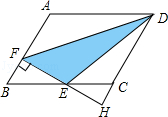
查看答案和解析>>
科目:初中数学 来源: 题型:
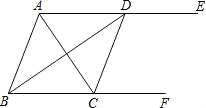
【题目】如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,AC=6,求AE,BF之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°,F是AC的中点,过AC上一点D作DE//AB,交BF的延长线于点E,AG⊥BE,垂足是G,连接BD、AE.
(1)求证:△ABC∽△BGA;
(2)若AF=5,AB=8,求FG的长;
(3)当AB=BC,∠DBC=30°时,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰RtABC 中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为8cm2,则△BPC的面积为( )

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列做法正确的是( )
A. 由2(x+1)=x+7去括号、移项、合并同类项,得x=5
B. 由![]() =1+
=1+![]() 去分母,得2(2x﹣1)=1+3(x﹣3)
去分母,得2(2x﹣1)=1+3(x﹣3)
C. 由2(2x﹣1)﹣3(x﹣3)=1去括号,得4x﹣2﹣3x﹣9=1
D. 由7x=4x﹣3移项,得7x﹣4x=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E. 
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com