
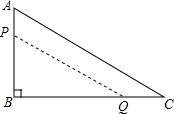
 如图,在ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动,动点Q从点B开始沿边BC向C以4mm/s的速度移动,如果P、Q分别从A、B同时出发,那么PBQ的面积S随出发时间t如何变化?写出函数关系式及t的取值范围.
如图,在ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动,动点Q从点B开始沿边BC向C以4mm/s的速度移动,如果P、Q分别从A、B同时出发,那么PBQ的面积S随出发时间t如何变化?写出函数关系式及t的取值范围. 分析 根据题意可以分别得到BP和BQ的长,从而可表示出三角形PBQ的面积,从而可以明确PBQ的面积S随出发时间t如何变化以及S以t的函数关系式及t的取值范围.
解答 解:由题意可得,
BP=AB-AP=12-2t,BQ=4t,
∴${S}_{△PBQ}=\frac{BP•BQ}{2}=\frac{(12-2t)•4t}{2}$=-4t2+24t=-4(t-3)2+36,
即当0≤t≤3时,PBQ的面积S随出发时间t的增大而增大,
当3≤t≤6时,PBQ的面积S随出发时间t的增大而减小,
即S=-4(t-3)2+36,t的取值范围是0≤t≤6.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,列出相应的函数关系式,可以根据函数关系式判断随着自变量的变化相应的函数图象如何变化.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:解答题
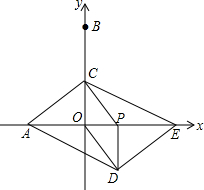 如图,在平面直角坐标系中,点A、B的坐标分别是(-2,0)、(0,4).动点P从O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止,点C停止运动时点P也随之停止运动.以CP、CO为邻边构造?PCOD,在线段OP的延长线长取点E,使得PE=2.设点P的运动时间为t秒.
如图,在平面直角坐标系中,点A、B的坐标分别是(-2,0)、(0,4).动点P从O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止,点C停止运动时点P也随之停止运动.以CP、CO为邻边构造?PCOD,在线段OP的延长线长取点E,使得PE=2.设点P的运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
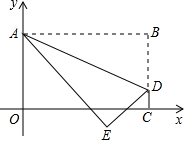 如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )
如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )| A. | $\frac{2}{5}<a<\frac{13}{20}$ | B. | $\frac{2}{5}<a<\frac{11}{20}$ | C. | $\frac{11}{20}<a<\frac{3}{5}$ | D. | $\frac{3}{5}<a<\frac{13}{20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,图①是棱长为4cm的立方体,沿其相邻三个面的对角线(虚线)裁掉一个角,得到如图②的几何体,则一只蚂蚁沿着图②几何体的表面,从顶点A爬到顶点B的最短距离为(2$\sqrt{2}$+2$\sqrt{6}$)cm.
如图,图①是棱长为4cm的立方体,沿其相邻三个面的对角线(虚线)裁掉一个角,得到如图②的几何体,则一只蚂蚁沿着图②几何体的表面,从顶点A爬到顶点B的最短距离为(2$\sqrt{2}$+2$\sqrt{6}$)cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com