
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
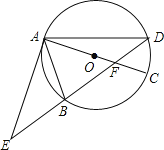
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似.
【答案】(1)见解析;(2)见解析.
【解析】
(1)连接CD,由AC是⊙O的直径,可得出∠ADC=90°,由角的关系可得出∠EAC=90°,即可得出EA是⊙O的切线;
(2)连接BC,由AC是⊙O的直径,可得出∠ABC=90°,由在Rt△EAF中,B是EF的中点,可得出∠BAC=∠AFE,即可得出△EAF∽△CBA.
(1)如图1,连接CD.
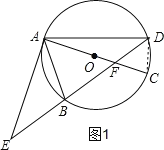
∵AC是⊙O的直径,∴∠ADC=90°,∴∠ADB+∠EDC=90°.
∵∠BAC=∠EDC,∠EAB=∠ADB,∴∠EAC=∠EAB+∠BAC=90°,∴EA是⊙O的切线.
(2)如图2,连接BC,
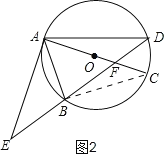
∵AC是⊙O的直径,∴∠ABC=90°,∴∠CBA=∠EAF=90°.
∵B是EF的中点,∴在Rt△EAF中,AB=BF,∴∠BAC=∠AFE,∴△EAF∽△CBA.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c中,4a﹣b=0,a﹣b+c>0,抛物线与x轴有两个不同的交点,且这两个交点之间的距离小于2.则下列结论:①abc<0,②c>0,③a+b+c>0,④4a>c,其中,正确结论的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )
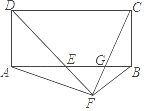
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD和菱形BEFG中,点A、B、G共线,点C在BE上,∠DAB=60°,AG=8,点M,N分别是AC和EG的中点,则MN的最小值等于( )
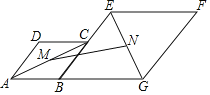
A.2![]() B.4C.2
B.4C.2![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给![]() 人.
人.
(1)求第一轮后患病的人数;(用含![]() 的代数式表示)
的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
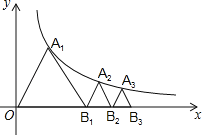
【题目】如图,已知等边△OA1B1,顶点A1在双曲线y=![]() (x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.
(x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
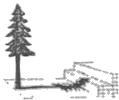
【题目】在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得落在教学楼第一级台阶上的影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为_____米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com