
【题目】如图,在△ABO中,已知点 ![]() 、B(﹣1,﹣1)、O(0,0),正比例函数y=﹣x图象是直线l,直线AC∥x轴交直线l与点C.
、B(﹣1,﹣1)、O(0,0),正比例函数y=﹣x图象是直线l,直线AC∥x轴交直线l与点C. 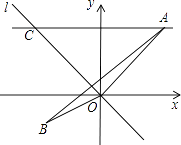
(1)C点的坐标为;
(2)以点O为旋转中心,将△ABO顺时针旋转角α(90°≤α<180°),使得点B落在直线l上的对应点为B′,点A的对应点为A′,得到△A′OB′. ①∠α=;②画出△A′OB′.
(3)写出所有满足△DOC∽△AOB的点D的坐标.
【答案】
(1)(﹣3,3)
(2)90°
(3)解:∵A点坐标可知OA与x轴正半轴夹角为60°,可知∠AOB=165°,
根据对应关系,则∠DOC=165°,故OD在第四象限,与x轴正半轴夹角为30°或与y轴负半轴夹角为30°,
根据A、B、C三点坐标,
∴OA=2 ![]() 、OB=
、OB= ![]() 、OC=3
、OC=3 ![]() ,
,
∵ ![]() ,
,
∴DO= ![]() =
= ![]() =6
=6 ![]() ,
,
∴D点的横坐标为:3 ![]() ,或纵坐标为:﹣3
,或纵坐标为:﹣3 ![]() ,
,
∴D点坐标为(9,﹣3 ![]() ),(3
),(3 ![]() ,﹣9).
,﹣9).
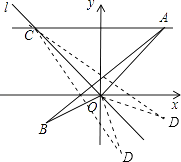

【解析】解:(1)∵直线AC∥x轴交直线l于点C, ∴A、C两点纵坐标为3,代入直线y=﹣x中,得C点横坐标为﹣3,
∴C(﹣3,3);(2)由B(﹣1,﹣1)可知,OB为第三象限角平分线,
又直线l为二、四象限角平分线,
∴旋转角为∠α=∠BOB′=90°,△A′OB′如图所示;
【考点精析】关于本题考查的一次函数的性质和相似三角形的判定与性质,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是 ![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1为平地上一幢建筑物与铁塔图,图2为其示意图.建筑物AB与铁塔CD都垂直于地面,BD=30m,在A点测得D点的俯角为45°,测得C点的仰角为60°.求铁塔CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() ,当自变量x取m时对应的值大于0,当自变量x分别取m﹣1、m+1时对应的函数值为y1、y2 , 则y1、y2必须满足( )
,当自变量x取m时对应的值大于0,当自变量x分别取m﹣1、m+1时对应的函数值为y1、y2 , 则y1、y2必须满足( )
A.y1>0、y2>0
B.y1<0、y2<0
C.y1<0、y2>0
D.y1>0、y2<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图(1),在Rt△ACB中,∠ACB=90°,AC=CB,∠DCE=45°,试探究AD、DE、EB满足的等量关系.
[探究发现]
小聪同学利用图形变换,将△CAD绕点C逆时针旋转90°得到△CBH,连接EH,由已知条件易得∠EBH=90°,∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°.
根据“边角边”,可证△CEH≌ , 得EH=ED.
在Rt△HBE中,由定理,可得BH2+EB2=EH2 , 由BH=AD,可得AD、DE、EB之间的等量关系是 .
[实践运用]
(1)如图(2),在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等,求∠EAF的度数;
(2)在(1)条件下,连接BD,分别交AE、AF于点M、N,若BE=2,DF=3,BM=2![]() ,运用小聪同学探究的结论,求正方形的边长及MN的长.
,运用小聪同学探究的结论,求正方形的边长及MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴( )
A.只能是x=﹣1
B.可能是y轴
C.可能在y轴右侧且在直线x=2的左侧
D.可能在y轴左侧且在直线x=﹣2的右侧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年是中国人民抗日战争暨世界反法西斯战争胜利70周年,9月3日全国各地将举行有关纪念活动.为了解初中学生对二战历史的知晓情况,某初中课外兴趣小组在本校学生中开展了专题调查活动,随机抽取了部分学生进行问卷调查,根据学生的答题情况,将结果分为A、B、C、D四类,其中A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”;D类表示“不太了解”,调查的数据经整理后形成尚未完成的条形统计图(如图①)和扇形统计图(如图②):
(1)在这次抽样调查中,一共抽查了 名学生
(2)请把图①中的条形统计图补充完整。
(3)求出D类的百分数,即可求出圆心角的度数。
(4)如果这所学校共有初中学生1500名,请你估算该校初中学生中对二战历史“非常了解”和“比较了解”的学生共有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com