
如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
(1)求证:DA=DC;
(2)⊙O的半径为3,AC=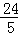 ,求GC的长.
,求GC的长.
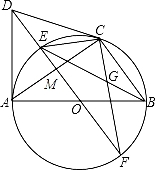
【考点】切线的性质;全等三角形的判定与性质;相似三角形的判定与性质.
【分析】(1)由AB是⊙O的直径,AB⊥DA,可得AD是⊙O的切线,又由DC是⊙O切线,根据切线长定理即可求得答案;
(2)由勾股定理求出EG、CF、BC长,根据△BGC∽△FGE求出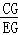 =
=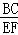 =
= =
=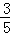 ,则CG=
,则CG=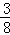 CF;利用勾股定理求出CF的长,则CG的长度可求得.
CF;利用勾股定理求出CF的长,则CG的长度可求得.
【解答】(1)证明:∵AB是⊙O的直径,AB⊥DA,
∴AD是⊙O的切线,
∵DC是⊙O切线,
∴DA=DC.
(2)解:由切线长定理得:DO垂直平方AC,
∵AC=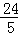 ,
,
∴AM=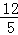 ,
,
在RT△MAO中,OM=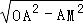 =
= =
=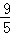 ,
,
∴EM=3﹣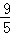 =
=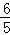 ,
,
在RT△EMC中,CE=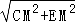 =
=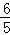
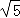 ,
,
∵EF是直径,
∴∠ECF=90°,
∴CF=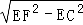 =
=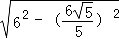 =
=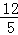
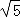 ,
,
∵AB是直径,
∴∠ACB=90°,
∴BC=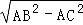 =
=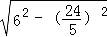 =
=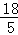 ,
,
∵∠GCB=∠GEF,∠GFE=∠GBC,(圆周角定理)
∴△BGC∽△FGE,
∴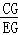 =
=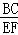 =
= =
=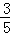 ,
,
∵CF=CG+GF,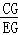 =
=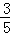 ,
,
∴CG=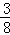 CF=
CF=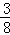 ×
×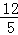
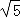 =
=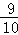
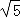 .
.
【点评】本题考查了切线的判定和性质,切线长定理,勾股定理,相似三角形的性质和判定,圆周角定理等知识点的应用,主要考查学生综合运用定理进行推理和计算的能力,综合性比较强,难度偏大.


科目:初中数学 来源: 题型:
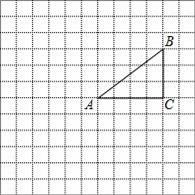
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件中,是随机事件的是( )
A.度量四边形的内角和为180°
B.通常加热到100℃,水沸腾
C.袋中有2个黄球,3个绿球,共五个球,随机摸出一个球是红球
D.抛掷一枚硬币两次,第一次正面向上,第二次反面向上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com