
【题目】如图,在△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分别是D、E、F.
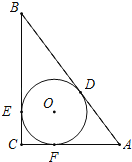
(1)连接OA、OB,则∠AOB= .
(2)若BD=6,AD=4,求⊙O的半径r.
【答案】(1)135°;(2)r=2
【解析】
(1)根据三角形的内心的性质即可解答.
(2)连接![]() ,根据圆的切线的性质和角平分线的性质,加之
,根据圆的切线的性质和角平分线的性质,加之![]() 为直角证明四边形
为直角证明四边形![]() 为正方形,设
为正方形,设![]() ,用
,用![]() 表示出
表示出![]() 的三边,运用勾股定理列方程解答即可.
的三边,运用勾股定理列方程解答即可.
解:(1)
∵⊙O是△ABC的内切圆,
∴O为△ACB的内心,
∴∠OBA=![]() ∠ABC,∠OAB=
∠ABC,∠OAB=![]() ∠CAB,
∠CAB,
∵∠C=90°,
∴∠CAB+∠CBA=90°,
∴∠OBA+∠OAB=![]() ×90°=45°,
×90°=45°,
∴∠AOB=180°﹣∠45°=135°,
故答案为:135°;
(2)连接EO,FO,
∵⊙O是△ABC的内切圆,切点分别为D,E,F,
∴OE⊥BC,OF⊥AC,BD=BE,AD=AF,EC=CF,
又∵∠C=90°,
∴四边形ECFO是矩形,
又∵EO=FO,
∴矩形OECF是正方形,
设EO=x,
则EC=CF=x,
在Rt△ABC中
BC2+AC2=AB2
故(x+6)2+(x+4)2=102,
解得:x=2,
即⊙O的半径r=2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=6,BC=8,若AC,BC边上的中线BE,AD 垂直相交于点O,则AB=( )

A. 5 B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你仔细观察下面一组图形,依据其变化规律推断第(5)个图形中所有正方形面积之和为____________(其中图 中出现的三角形均是直角三角形,四边形均是正方形).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】熊组长准备为我们年级投资1万元围一个矩形的运动场地(如图),其中一边靠墙,另外三边选用不同材料建造且三边的总长为![]() ,墙长
,墙长![]() ,平行于墙的边的费用为200元/
,平行于墙的边的费用为200元/![]() ,垂直于墙的边的费用150元/
,垂直于墙的边的费用150元/![]() ,设平行与墙的边长为
,设平行与墙的边长为![]() .
.
(1)若运动场地面积为![]() ,求
,求![]() 的值;
的值;
(2)当运动场地的面积最大时是否会超了预算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与原点重合,
与原点重合,![]() 、
、![]() 分别在坐标轴上,
分别在坐标轴上,![]() ,
,![]() ,直线
,直线![]() 交
交![]() ,
,![]() 分别于点
分别于点![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,
,![]() .
.
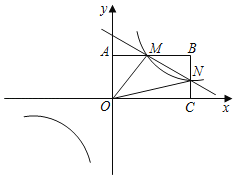
(1)求反比例函数的解析式;
(2)直接写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)若点![]() 在
在![]() 轴上,且
轴上,且![]() 的面积与四边形
的面积与四边形![]() 的面积相等,求点
的面积相等,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产的一种果汁饮料由A、B两种水果配制而成,其比例与成本如下方表格所示,已知该饮料的成本价为8元/千克,按现价售出后可获利润50%,每个月可出售27500瓶.
每千克饮料所占比例 | 成本(元/千克) | |
A | 20% | m |
B | 80% | m-15 |
(1)求m的值;
(2)由于物价上涨,A水果成本提高了25%,B水果成本提高了20%,在不改变售价的情况下,若要保持每个月的利润不减少,则现在至少需要售出多少瓶饮料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=4![]() ,把边CD绕点C逆时针旋转30度得到线段CE,连接BE并延长,交AD于点F,连接DE,则线段EF的长度为________
,把边CD绕点C逆时针旋转30度得到线段CE,连接BE并延长,交AD于点F,连接DE,则线段EF的长度为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=50°,则∠BDE= °.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com