
【题目】如图,在![]() 中,
中,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿折线
的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒(
秒(![]() ).
).
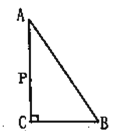
(1)用尺规作线段![]() 的垂直平分线(不写作法,保留作图痕迹);
的垂直平分线(不写作法,保留作图痕迹);
(2)若点![]() 恰好运动到
恰好运动到![]() 的垂直平分线上时,求
的垂直平分线上时,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】如图,已知直线lAC:y=﹣![]() 交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.
交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.
(1)求点B的坐标及直线BC的解析式;
(2)将△OBC关于BC边翻折,得到△O′BC,过点O′作直线O′E垂直x轴于点E,F是y轴上一点,P是直线O′E上任意一点,P、Q两点关于x轴对称,当|PA﹣PC|最大时,请求出QF+![]() FC的最小值;
FC的最小值;
(3)若M是直线O′E上一点,且QM=3![]() ,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,DE分别是边AB、AC上的点,且AD=CE,则∠ADC+∠BEA=( )
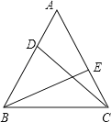
A.180°B.170°C.160°D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一家糖果加工厂,它们要对一款奶糖进行包装,要求每袋净含量为100g.现使用甲、乙两种包装机同时包装100g的糖果,从中各抽出10袋,测得实际质量(g)如下:
甲:101,102,99,100,98,103,100,98,100,99
乙:100,101,100,98,101,97,100,98,103,102
(1)分别计算两组数据的平均数、众数、中位数;
(2)要想包装机包装奶糖质量比较稳定,你认为选择哪种包装机比较适合?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() 都为等腰直角三角形,
都为等腰直角三角形,![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() .
.

(1)若![]() ,求
,求![]() 的周长;
的周长;
(2)如图![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长至
并延长至![]() ,使得
,使得![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
②探索![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 于E,
于E,![]() ,D是AE上的一点,且
,D是AE上的一点,且![]() ,连接BD,CD.
,连接BD,CD.

![]() 试判断BD与AC的位置关系和数量关系,并说明理由;
试判断BD与AC的位置关系和数量关系,并说明理由;
![]() 如图2,若将
如图2,若将![]() 绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
![]() 如图3,若将
如图3,若将![]() 中的等腰直角三角形都换成等边三角形,其他条件不变.
中的等腰直角三角形都换成等边三角形,其他条件不变.
![]() 试猜想BD与AC的数量关系,请直接写出结论;
试猜想BD与AC的数量关系,请直接写出结论;
![]() 你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
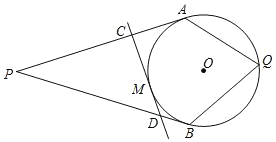
【题目】如图,PA、PB分别切⊙O于点A、B,M为劣弧AB上一点(不与A、B重合)过点M的切线分别与PA、PB相交于点C、D,Q为优弧AB上一点(不与A、B重合).
(1)若PA=10,求△PCD的周长;
(2)若∠P=40°,求∠AQB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了![]() ,
,![]() 两种型号的空气净化器,已知一台
两种型号的空气净化器,已知一台![]() 型空气净化器的进价比一台
型空气净化器的进价比一台![]() 型空气净化器的进价多300元,用7500元购进
型空气净化器的进价多300元,用7500元购进![]() 型空气净化器和用6000元购进
型空气净化器和用6000元购进![]() 型空气净化器的台数相同.
型空气净化器的台数相同.
(1)求一台![]() 型空气净化器和一台
型空气净化器和一台![]() 型空气净化器的进价各为多少元?
型空气净化器的进价各为多少元?
(2)在销售过程中,![]() 型空气净化器因为净化能力强,噪声小而更受消费者的欢迎.商社电器计划
型空气净化器因为净化能力强,噪声小而更受消费者的欢迎.商社电器计划![]() 型净化器的进货量不少于20台且是
型净化器的进货量不少于20台且是![]() 型净化器进货量的三倍,在总进货款不超过5万元的前提下,试问有多少种进货方案?
型净化器进货量的三倍,在总进货款不超过5万元的前提下,试问有多少种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“均衡教育大检查”,县委县府对通往某偏远学校的一段全长为1200 米的道路进行了改造,铺设草油路面.铺设400 米后,为了尽快完成道路改造,后来每天的工作效率比原计划提高25%,结果共用13天完成道路改造任务.
(1)求原计划每天铺设路面多少米;
(2)若承包商原来每天支付工人工资为1500元,提高工作效率后每天支付给工人的工资增长了20%,完成整个工程后承包商共支付工人工资多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com