
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵxOy�У�Rt��AOB��ֱ�DZ�OB��OA�ֱ���x���Ϻ�y���ϣ�����OA=2��OB=4���ֽ�Rt��AOB����ֱ�Ƕ���O����ʱ�뷽����ת90���õ���COD����֪һ�����߾���C��D��B���㣮
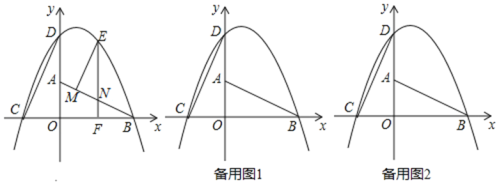
��1���������ߵĽ���ʽΪ������
��2�����E����������λ�ڵ�һ���Ķ��㣬����E��EF��x���ڵ�F������ֱ��AB��N������E����EM��AB�ڵ�M������EMN�ܳ������ֵ��
��3������EMN���ܳ����ʱ����ֱ��EF���Ƿ���ڵ�Q��ʹ����QCD����CDΪֱ�DZߵ�ֱ�������Σ��������������Q�����꣬�������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() +x+4����2�����ֵΪ
+x+4����2�����ֵΪ![]() ����3�����ڣ�����Q������Ϊ��
����3�����ڣ�����Q������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ��ʱ��ʹ����QCD����CDΪֱ�DZߵ�ֱ��������
��ʱ��ʹ����QCD����CDΪֱ�DZߵ�ֱ��������
��������
��1���������ߵĽ���ʽΪ![]() �����߶�OA��OB�ij��ȿɵó���A��B�����꣬������ת�����Կɵó���C��D�����꣬�ɵ�B��C��D������������ô���ϵ����������������ߵĽ���ʽ��
�����߶�OA��OB�ij��ȿɵó���A��B�����꣬������ת�����Կɵó���C��D�����꣬�ɵ�B��C��D������������ô���ϵ����������������ߵĽ���ʽ��
��2����Rt��AOB�У������ABO����������ֵ���ٸ������������ε��ж������ҳ���EMN�ס�BFN���Ӷ��ó���MEN=��FBN����EN�ij�������ʾ��EM��MN�ij��ȣ��ɵ�A��B���������ô���ϵ�������ֱ��AB�ĺ�������ʽ�������E������Ϊ![]() ��0��t��4���������ҳ���N������Ϊ
��0��t��4���������ҳ���N������Ϊ![]() ���Ӷ��ó��߶�EN�ij��ȣ���EN��MN��EM��Ӽ��ɵó���EMN���ܳ������ݶ��κ��������ʿ����EN�����ֵ���ɴ˼��ɵó����ۣ�
���Ӷ��ó��߶�EN�ij��ȣ���EN��MN��EM��Ӽ��ɵó���EMN���ܳ������ݶ��κ��������ʿ����EN�����ֵ���ɴ˼��ɵó����ۣ�
��3����ϣ�2���Ľ��ۿ�ֱ֪��EF�Ľ���ʽΪ![]() ���֡�QDC=90��͡�DCQ=90��������������ǣ��������������ε������ҳ����Ʊߵı�����ϵ���ҳ��߶εij��ȣ��ٸ��ݵ������������ϵ�����ҳ���Q�����꣮
���֡�QDC=90��͡�DCQ=90��������������ǣ��������������ε������ҳ����Ʊߵı�����ϵ���ҳ��߶εij��ȣ��ٸ��ݵ������������ϵ�����ҳ���Q�����꣮
�⣺��1���������ߵĽ���ʽΪ![]() ��
��
��OA=2��OB=4��
���A��0��2������B��4��0����
����ת�����Կ�֪��
��C����2��0������D��0��4����
����B��4��0������C����2��0������D��0��4�����뵽�����߽���ʽ�ã�
 ����ã�
����ã� ��
��
��������ߵĽ���ʽΪ![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2���������⻭��ͼ�Σ���ͼ1��ʾ��
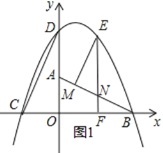
��Rt��AOB��OA=2��OB=4��
��AB=![]()
![]() ��
��
��sin��ABO=![]() ��cos��ABO=
��cos��ABO=![]() ��
��
��EM��AB��EF��OB��
���EMN=��BFN=90����
�ߡ�BNF=��ENM��
���EMN�ס�BFN��
���MEN=��FBN��
��Rt��EMN��sin��MEN=![]() ��cos��MEN=
��cos��MEN=![]() ��
��
��MN=ENsin��MEN=ENsin��ABO=![]() EN��
EN��
EM=ENcos��MEN=ENcos��ABO=![]() EN��
EN��
��C��EMN=EM+MN+EN=![]() EN+
EN+![]() EN+EN=
EN+EN=![]() EN��
EN��
�ɣ�1��֪A��0��2����B��4��0������ֱ��AB�Ľ���ʽΪ��y=kx+2��
��4k+2=0����ã�k=![]() ��
��
��ֱ��AB�Ľ���ʽΪ��![]() ��
��
���������ϵ�E������Ϊ![]() ��0��t��4����
��0��t��4����
��EF��OB��
����y=![]() +2��x=t��y=
+2��x=t��y=![]() +2��
+2��
���N��������t����![]() t+2����
t+2����
��EN=��![]() +t+4������
+t+4������![]() t+2��=��
t+2��=��![]() +
+![]() t+2��
t+2��
��C��EMN=![]() ����
����![]() +
+![]() t+2��=��
t+2��=��![]()
![]() ��0��t��4����
��0��t��4����
�൱![]() ʱ��EN���ʱC��EMN���
ʱ��EN���ʱC��EMN���
��C��EMN�����![]() [��
[��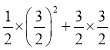 +2]=
+2]=![]() ��
��
��3���ɣ�2��֪����C��EMNȡ���ֵʱ��EF�Ľ���ʽΪ��x=![]() ��
��
������QDC=90��������Q��QG��y���ڵ�G����ͼ2��ʾ��
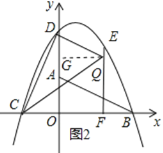
��EF�Ľ���ʽΪ��x=![]() ��
��
��QG=![]() ��
��
�ߡ�QDG+��DQG=90������CDO+��QDG=90����
���DGQ=��CDO��
�֡ߡ�QGD=��DOC=90����
���QDG�ס�DCO��
��![]() ��
��
��DG=2��![]() ��
��
��OG=OD��DG=4��![]() ��
��
���Q��������![]() ��
��![]() ����
����
������DCQ=90������ͼ3��ʾ��
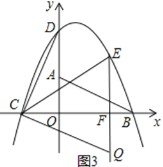
CF=![]() ������2��=
������2��=![]() ��
��
�ߡ�QCF+��OCD=90������CDO+��OCD=90����
���QCF=��CDO��
�֡ߡ�CFQ=��DOC=90����
���COD�ס�QFC��
��![]() ����
����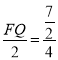 ��
��
��FQ=![]() ��
��
���Q��������![]() ��
��![]() ����
����
��������������Q��������![]() ��
��![]() ����
����![]() ��
��![]() ��ʱ��ʹ����QCD����CDΪֱ�DZߵ�ֱ�������Σ�
��ʱ��ʹ����QCD����CDΪֱ�DZߵ�ֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ҫ��Ӫһ�������е��ľߣ�����Ϊ20Ԫ����Ӫ���η��֣������۵�����25Ԫʱ��ÿ���������Ϊ250�������۵���ÿ����1Ԫ��ÿ����������ͼ���10��
��1��д���̳����������ľߣ�ÿ�����õ���������![]() ��Ԫ�������۵���
��Ԫ�������۵���![]() ��Ԫ��֮��ĺ�����ϵʽ��
��Ԫ��֮��ĺ�����ϵʽ��
��2�������۵���Ϊ����Ԫʱ�����ľ�ÿ��������������
��3���̳���Ӫ���������������������A��B����Ӫ������
����A�����ľߵ����۵��۸��ڽ����Ҳ�����30Ԫ��
����B��ÿ��������������10������ÿ���ľߵ���������Ϊ25Ԫ
��Ƚ����ַ��������������ߣ���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��ͨ����ͼ���֣�����
��ͨ����ͼ���֣�����![]() ȡ��ֵ���������ܻᾭ����������
ȡ��ֵ���������ܻᾭ����������
![]() ֱ��д����������������� �� ��
ֱ��д����������������� �� ��
![]() ����������������ƽ��
����������������ƽ��![]() ����λ��������ƽ��
����λ��������ƽ��![]() ����λ��ƽ�ƺ�������߶��㶼��ij��������ͼ���ϣ�������º����Ľ���ʽ(����д�Ա���ȡֵ��Χ)��
����λ��ƽ�ƺ�������߶��㶼��ij��������ͼ���ϣ�������º����Ľ���ʽ(����д�Ա���ȡֵ��Χ)��
![]() ��������
��������![]() ��ֱ��
��ֱ��![]() ����������
����������![]() ��
��![]() ����
����![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() �ύ�ڵ�(0��3)��
�ύ�ڵ�(0��3)��
��1����![]() ��ֵ����������
��ֵ����������![]() ��Ľ������ꣻ
��Ľ������ꣻ
��2��![]() ȡʲôֵʱ����������
ȡʲôֵʱ����������![]() ���·���
���·���
��3��![]() ȡʲôֵʱ��
ȡʲôֵʱ��![]() ��ֵ����
��ֵ����![]() �����������
�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ŷ����Ǵ��ϲ����һ���˶��������������С�����������㳡�Ϸŷ��ݣ���ͼ������A����С���÷��ݹ�����һ�������ϣ����ݹ̶�����D������ʱ������AD��ˮƽ�ߵļн�Ϊ30�㣬Ϊ�˱��ڹ۲죬С��Ѹ����ǰ���ƶ������ߵ�������A��10��B������ʱ������BD��ˮƽ�ߵļн�Ϊ45�㣮��֪��A��B��C��ͬһ��ˮƽֱ���ϣ��������С����ʱ���ջصķ����ߵij����Ƕ����ף���������AD��BD��Ϊ�߶Σ�![]() ��1.414��
��1.414��![]() ��1.732���������ȷ��1�ף���
��1.732���������ȷ��1�ף���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
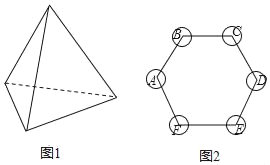
����Ŀ��ͼ����һö�ʵؾ��ȵ�����������״�����ӣ�ÿ�����Ϸֱ��������2��3��4��5��ͼ����һ�������������̣���ͨ�������ӵķ�ʽ��������Ϸ�������ǣ�����ö�����������������������������ϣ������棩�������Ǽ����ʹ�ͼ�е�A�㿪ʼ����˳ʱ�뷽�����������������㣬�ڶ��δӵ�һ�ε��յ㴦��ʼ������һ�εķ�����������
��1�������һ�����ӣ���������������C���ĸ������� ����
��2��������������ӣ��û���״ͼ���б��ķ�����������������������C���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
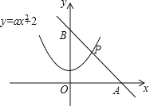
����Ŀ����ͼ��ֱ��l����A(4��0)�͵�B(0��4)��������κ���y��ax2��2��ͼ���ڵ�P������AOP�����Ϊ![]() ������κ����ı���ʽ��
������κ����ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��
��![]() ��
��![]() �IJ��ֶ�Ӧֵ���±���ʾ��
�IJ��ֶ�Ӧֵ���±���ʾ��
| �� | -1 | 0 | 1 | 2 | 3 | 4 | �� |
| �� | 6 | 1 | -2 | -3 | -2 | m | �� |
�������ĸ��۶ϣ�
��������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ��
��
��![]() ��
��
�۹���![]() �ķ���
�ķ���![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ��
��
��![]() ��
��
���У���ȷ����___________________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����²��ϣ�����Ҫ�������Ӧ������
����������ŷ����Leonhard Euler������ʿ��ѧ�ң�����ѧ�Ͼ�������������������������Ҫ��������ʽ�Ͷ�����������ŷ�����ֵ�һ������������ABC �У�R �� r �ֱ�Ϊ���Բ������Բ�İ뾶��O �� I �ֱ�Ϊ�����ĺ����ģ���OI ![]() R
R![]() 2Rr .
2Rr .
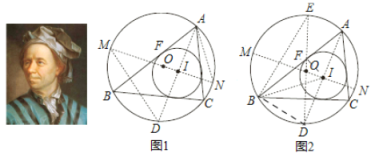
�����Ǹö�����֤�����̣������˵�(2)�ʵĽ��ۣ���
�ӳ�AI ����O �ڵ� D������ I ����O ��ֱ�� MN������ DM��AN.
�ߡ�D=��N�����DMI=��NAI��ͬ�����Ե�Բ�ܽ���ȣ���
���MDI�ס�ANI.��![]() ���� IA ID IM IN ��
���� IA ID IM IN ��
��ͼ�ڣ���ͼ 1����ȥ MD��AN���Ļ���������O ��ֱ��DE������BE��BD��BI��IF
��DE �ǡ�O ��ֱ�������DBE=90��.
�ߡ�I �� AB �����ڵ� F�����AFI=90����
���DBE=��IFA.
�ߡ�BAD=��E��ͬ������Բ�ܽ���ȣ���
���AIF�ס�EDB��
��![]() ����
����![]() �ڣ�
�ڣ�
�ɣ�2��֪��![]() ��
��
��![]()
�֡�![]() ��
��
�� 2Rr(R d )(R d ) ��
�� R![]() d
d![]() 2Rr
2Rr
�� d ![]() R
R![]() 2Rr
2Rr
����1���۲췢�֣� IM R d �� IN ���ú�R��d �Ĵ���ʽ��ʾ����
��2�����ж� BD �� ID ��������ϵ����˵������.��������ͼ 1 ֤����
��3��Ӧ�ã�����ABC �����Բ�İ뾶Ϊ 6cm������Բ�İ뾶Ϊ 2cm������ABC ������������֮��ľ���Ϊ ����cm��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com