
【题目】已知抛物线![]() ,通过画图发现,无论
,通过画图发现,无论![]() 取何值,抛物线总会经过两个定点
取何值,抛物线总会经过两个定点
![]() 直接写出这两个定点的坐标 、 ;
直接写出这两个定点的坐标 、 ;
![]() 若将此抛物线向右平移
若将此抛物线向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,平移后的抛物线顶点都在某个函数的图象上,求这个新函数的解析式(不必写自变量取值范围);
个单位,平移后的抛物线顶点都在某个函数的图象上,求这个新函数的解析式(不必写自变量取值范围);
![]() 若抛物线
若抛物线![]() 与直线
与直线![]() 有两个交点
有两个交点![]() 与
与![]() .且
.且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)抛物线![]() =b(x2+x)-3x-3,函数过定点,则x2+x=0,即可求解;
=b(x2+x)-3x-3,函数过定点,则x2+x=0,即可求解;
(2)原抛物线顶点坐标为(![]() ,
,![]() ),平移后为(
),平移后为(![]() ,
,![]() ),即可求解;
),即可求解;
(3)由![]() ,则1≤AB两点水平距离≤4,分当b>0时和当b<0时用韦达定理即可求解.
,则1≤AB两点水平距离≤4,分当b>0时和当b<0时用韦达定理即可求解.
解(1)∵![]() =b(x2+x)-3x-3, 函数过定点,
=b(x2+x)-3x-3, 函数过定点,
∴x2+x=0,解得,x=0或x=-1,
∴抛物线总会经过![]()
故答案为![]() ;
;
![]() 解:原抛物线顶点横坐标为:
解:原抛物线顶点横坐标为:![]()
纵坐标为:![]()
平移后新抛物线顶点横坐标为:![]()
纵坐标为:![]()
由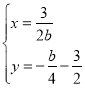
得:![]()
即为平移后的抛物线顶点所在的函数解析式.
(3)∵![]() ,则1≤AB两点水平距离≤4,
,则1≤AB两点水平距离≤4,
当b>0时,
设抛物线与直线交点为A与B,则A(0,-3),B(x,y),
∴![]() =x-3,整理得,bx2+(b-4)x=0,
=x-3,整理得,bx2+(b-4)x=0,
由韦达定理得,x+0=![]() ,则1≤
,则1≤![]() ≤4,
≤4,
解得:![]() ≤b≤2,
≤b≤2,
同理,当b<0时,解得:![]()
综上所述,![]() 的取值范围为
的取值范围为![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共有19条运营线路,覆盖北京市11个辖区.据统计,2017 年地铁每小时客运量是2002年地铁每小时客运量的4倍,2017年客运240万人所用的时间比2002年客运240万人所用的时间少30小时,求2017年地铁每小时的客运量?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便游客观赏景点,某景区设计建造了如图所示的高为6米的观景台![]() ,且坡面
,且坡面![]() 的坡度比为1:1.后来为了方便行人推车(如子女带老人旅游等),决定降低坡度,新坡面的坡度比为
的坡度比为1:1.后来为了方便行人推车(如子女带老人旅游等),决定降低坡度,新坡面的坡度比为![]() .
.
(1)求新坡面的坡角![]() .
.
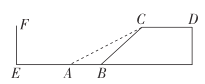
(2)原坡面底部的正前方13米(![]() 的长)有一座古建筑
的长)有一座古建筑![]() ,为保护文物,当地文物管理部门规定,坡面底部至少距古建筑7米,请问新的设计方案能否通过,试说明理由.(参考数据:
,为保护文物,当地文物管理部门规定,坡面底部至少距古建筑7米,请问新的设计方案能否通过,试说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某工厂为全运会设计了一款成本每件20元的工艺品,投放市场试销后发现销售量y(件)是售价x(元/件)的一次函数,当售价为23元/件时,每天销售量为790件;当售价为25元/件,每天销售量为750件.
(1)求y与x的函数关系;
(2)如果该工艺品最高不超过每件30元,那么售价定位每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
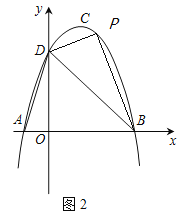
【题目】如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
(1)求抛物线的解析式;
(2)如图2,点P为直线BD上方抛物线上一点,若![]() ,请求出点P的坐标.
,请求出点P的坐标.
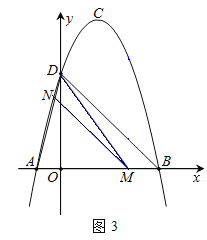
(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.
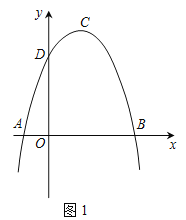
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xOy中,Rt△AOB的直角边OB,OA分别在x轴上和y轴上,其中OA=2,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.
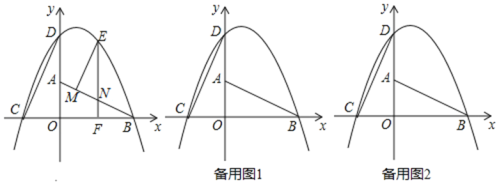
(1)该抛物线的解析式为 ;
(2)设点E是抛物线上位于第一象限的动点,过点E作EF⊥x轴于点F,并交直线AB于N,过点E再作EM⊥AB于点M,求△EMN周长的最大值;
(3)当△EMN的周长最大时,在直线EF上是否存在点Q,使得△QCD是以CD为直角边的直角三角形?若存在请求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com