
【题目】如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
(1)求抛物线的解析式;
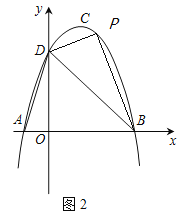
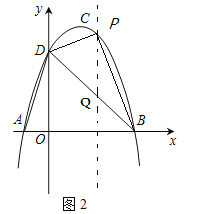
(2)如图2,点P为直线BD上方抛物线上一点,若![]() ,请求出点P的坐标.
,请求出点P的坐标.
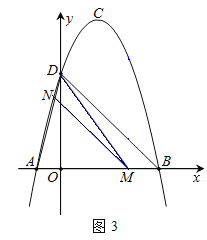
(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.
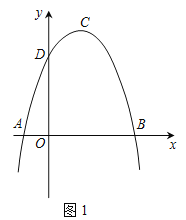
【答案】(1)y=-x2+2x+3;(2)点P的坐标为(1,4)或(2,3);(3)点M的坐标为(![]() ,0).
,0).
【解析】
(1)设抛物线的解析式为:y=a(x-1)2+4,然后将点B的坐标代入函数解析式即可求得此抛物线的解析式;
(2)如图2,过点P作PQ//y轴交DB于Q,求出直线BD的解析式,设P(m, -m2+2m+3),则Q(m,-m+3),得到S△PBD =-![]() m2+
m2+![]() m,又
m,又![]() ,解方程求出m的值,再求点P的坐标即可;
,解方程求出m的值,再求点P的坐标即可;
(3)设M(c,0),由△AMN∽△AMD,得到![]() ,得出MN=
,得出MN=![]() ,DM=
,DM=![]() ,再由△DNM∽△BMD,得到
,再由△DNM∽△BMD,得到![]() ,即9+c2=
,即9+c2=![]() ×
×![]() ,求解即可的出答案.
,求解即可的出答案.
(1)设所求抛物线的解析式为:y=a(x-1)2+4,
将点B(3,0)代入,得:(3-1)2a+4=0
解得:a=-1
∴解析式为:y=-(x-1)2+4=-x2+2x+3
(2)如图2,过点P作PQ//y轴交DB于Q,
∵抛物线的解析式为y=-x2+2x+3,
∴点D的坐标为(0,3),
设直线BD的解析式为y=kx+b,
把D(0,3)和B(3,0)代入y=kx+b得,![]() ,
,
解得:![]()
∴直线BD的解析式为y=-x+3,
设P(m, -m2+2m+3),则Q(m,-m+3).
∴PQ=-m2+2m+3(-m+3)= -m2+3m,
又∵S△PBD=S△PQD+S△PQB
=![]() mPQ+
mPQ+![]() (3m)PQ=
(3m)PQ=![]() PQ×3=
PQ×3=![]()
![]() m2+
m2+![]() m,
m,
∵![]() ,
,
∴-![]() m2+
m2+![]() m=3
m=3
解得:m1=1,m2=2,
∴点P的坐标为(1,4)或(2,3)
(3) ∵BD=![]() ,设M(c,0),
,设M(c,0),
∵MN∥BD,
∴△AMN∽△AMD,
∴![]() ,即
,即![]() ,
,
∴MN=![]() ,DM=
,DM=![]() ,
,
∵△DNM∽△BMD,
∴![]() ,即DM2=BD·MN,
,即DM2=BD·MN,
∴9+c2=![]() ×
×![]() ,
,
解得:c=![]() 或c=3(舍去),
或c=3(舍去),
∴点M的坐标为(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜市场为指导某种蔬菜的生产和销售,对往年的市场行情和生产情况进行了调查,提供的信息如下:
信息1:售价和月份满足一次函数关系,如下表所示.
月份 | … | 3 | 6 | … |
售价 | … | 5 | 3 | … |
信息2:成本和月份满足二次函数关系,并且知道该种蔬菜在6月成本达到最低为1元/千克,9月成本为4元/千克.
根据以上信息回答下列问题:
(1)在7月,这种蔬菜的成本是多少元每千克?
(2)在过去的一年中,某商家平均每天卖出![]() 该种蔬菜,则哪个月的利润最大,最大利润为多少?(一个月按30天计算)
该种蔬菜,则哪个月的利润最大,最大利润为多少?(一个月按30天计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某飞机场东西方向的地面 l 上有一长为 1km 的飞机跑道 MN(如图),在跑道 MN的正西端 14.5 千米处有一观察站 A.某时刻测得一架匀速直线降落的飞机位于点 A 的北偏西30°,且与点 A 相距 15 千米的 B 处;经过 1 分钟,又测得该飞机位于点 A 的北偏东 60°,且与点 A 相距 5![]() 千米的 C 处.
千米的 C 处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道 MN 之间?请说明理由.
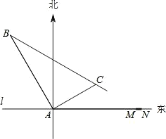
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 点
点![]() 与点
与点![]() 在
在![]() 的同侧,且
的同侧,且![]() .
.

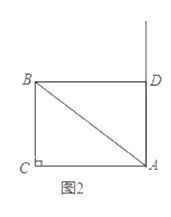
(1)如图1,点![]() 不与点
不与点![]() 重合,连结
重合,连结![]() 交
交![]() 于点
于点![]() .设
.设![]() 求
求![]() 关于
关于![]() 的函数解析式,写出自变量
的函数解析式,写出自变量![]() 的取值范围;
的取值范围;
(2)是否存在点![]() ,使
,使![]() 与
与![]() 相似,若存在,求
相似,若存在,求![]() 的长;若不存在,请说明理由;
的长;若不存在,请说明理由;
(3)如图2,过点![]() 作
作![]() 垂足为
垂足为![]() .将以点
.将以点![]() 为圆心,
为圆心,![]() 为半径的圆记为
为半径的圆记为![]() .若点
.若点![]() 到
到![]() 上点的距离的最小值为
上点的距离的最小值为![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在每个小正方形的边长为1的网格中,△ABC的顶点A、B、C均在格点上,点D为AC边上的一点.
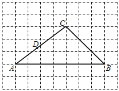
(1)线段AC的长为 .
(2)在如图所示的网格中,AM是△ABC的角平分线,在AM上求一点P,使CP+DP的值最小,请用无刻度的直尺,画出AM和点P,并简要说明AM和点P的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 所有矩形都是相似的
B. 若线段a=5cm,b=2cm,则a:b=5:2
C. 若线段AB=![]() cm,C是线段AB的黄金分割点,且AC>BC,则AC=
cm,C是线段AB的黄金分割点,且AC>BC,则AC=![]() cm
cm
D. 四条长度依次为lcm,2cm,2cm,4cm的线段是成比例线段
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com