
【题目】我省某工厂为全运会设计了一款成本每件20元的工艺品,投放市场试销后发现销售量y(件)是售价x(元/件)的一次函数,当售价为23元/件时,每天销售量为790件;当售价为25元/件,每天销售量为750件.
(1)求y与x的函数关系;
(2)如果该工艺品最高不超过每件30元,那么售价定位每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?
【答案】(1)函数的关系式为y=-20x+1250;
(2)当售价定为30元/时,该工艺品每天获得的利润最大,最大利润为6500元.
【解析】
(1)将x=23,y=790,x=25,y=750代入y=kx+b即可求得y与x的函数关系式;(2)先求得每天获得的利润w关于x的函数关系式,再求出当x=30时获得的利润最大.
解:(1)设y与x的函数关系式为y=kx+b(k≠0),
把x=23,y=790,x=25,y=750代入y=kx+b得![]() ,
,
解得![]() ,
,
∴函数的关系式为y=-20x+1250;
(2)设该工艺品每天获得的利润为W元,
则W=y(x-20)=(-20x+1250)(x-20)=-10(x-41.25) 2 +9031.25,(20≤x≤30);
∵-20<0,
∴当20<x≤30时,w随x的增大而增大.
所以当售价定为30元/件时,该工艺品每天获得的利润最大.
W 最大 =-20(30-41.25) 2 +9031.25=6500元.
答:当售价定为30元/时,该工艺品每天获得的利润最大,最大利润为6500元.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 经过点
经过点![]() ,
,![]() 、
、![]() ,
,![]() ,其中
,其中![]() 、
、![]() 是方程
是方程![]() 的两根,且
的两根,且![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线只有一个公共点
与抛物线只有一个公共点
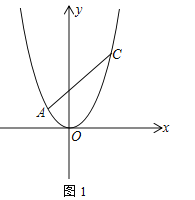
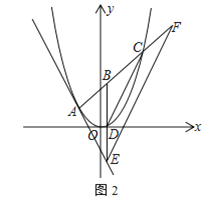
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)求直线![]() 的解析式;
的解析式;
(3)如图2,点![]() 是线段
是线段![]() 上的动点,若过点
上的动点,若过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与抛物线相交于点
,与抛物线相交于点![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求:菱形ABCD的面积.
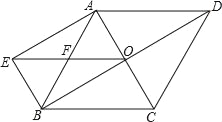
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠POQ=60°,点A、B分别在射线OQ、OP上,且OA=2,OB=4,∠POQ的平分线交AB于C,一动点N从O点出发,以每秒1个单位长度的速度沿射线OP向点B作匀速运动,MN⊥OB交射线OQ于点M.设点N运动的时间为t(0<t<2)秒.
(1)求证:△ONM∽△OAB;
(2)当MN=CM时,求t的值;
(3)设△MNC与△OAB重叠部分的面积为S.请求出S关于t的函数表达式.
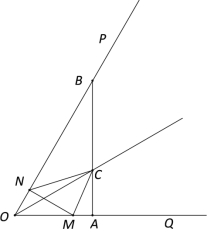
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是( )
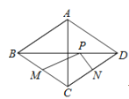
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
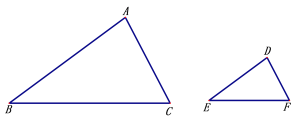
【题目】求证:相似三角形对应角的角平分线之比等于相似比.要求:
①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com