
【题目】如图,在![]() 中,半径
中,半径![]() 直径
直径![]() 与
与![]() 相切于点
相切于点![]() 连接
连接![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
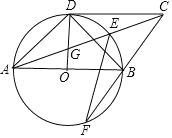
![]() 求证:
求证: ![]() ;
;
![]() 若
若![]()
①求证:四边形![]() 是平行四边形;
是平行四边形;
②连接![]() ,当
,当![]() 的半径为
的半径为![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)详见解析;(2)①详见解析;②![]()
【解析】
(1)先利用切线的性质得到OD⊥CD,再证明AB∥CD,然后利用平行线的性质和圆周角定理得到结论;
(2)①设⊙O的半径为r,利用正切的定义得到OG=![]() r,则DG=
r,则DG=![]() r,则CD=3DG=2r,然后根据平行线的判定得到结论;
r,则CD=3DG=2r,然后根据平行线的判定得到结论;
②作直径DH,连接HE,如图,先计算出AG=![]() ,CG=2
,CG=2![]() ,再证明△CDE∽△CAD,然后利用相似比计算DE的长.
,再证明△CDE∽△CAD,然后利用相似比计算DE的长.
![]() 证明:
证明: ![]() 与
与![]() 相切于点
相切于点![]() ,
,
![]() ,
,
![]() 半径
半径![]() 直径
直径![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 证明:
证明:![]() ,
,
![]()
设![]() 的半径为
的半径为![]() ,
,
在![]() 中,
中, ![]()
![]()
![]()
在![]() 中,
中,![]()
![]() ,
,
![]() ,
,
而![]() ,
,
![]() 四边形
四边形![]() 是平行四边形:
是平行四边形:
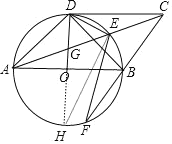
![]() 作直径
作直径![]() 连接
连接![]() ,如图,
,如图,
∵![]() ,半径为3
,半径为3
∴![]()
∵四边形![]() 是平行四边形,OD⊥CD,
是平行四边形,OD⊥CD,
∴![]() ,
,
![]() 为直径,
为直径,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
而![]()
![]() ,
,
![]() ,即
,即![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】为改善生态环境,建设美丽乡村,某村规划将一块长18米,宽10米的矩形场地建设成绿化广场,如图,内部修建三条宽相等的小路,其中一条路与广场的长平行,另两条路与广场的宽平行,其余区域种植绿化,使绿化区域的面积为广场总面积的80%.
(1)求该广场绿化区域的面积;
(2)求广场中间小路的宽.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
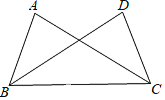
A.∠A=∠DB.∠ACB=∠DBCC.AC=DBD.AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
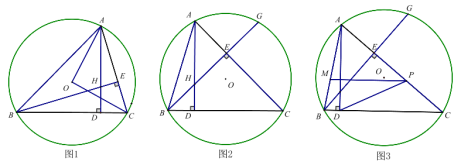
【题目】已知,△ABC内接于⊙O,AD⊥BC于D,BE⊥AC于E,AD、BE交于点H.
(1)如图1,连接OA、OC,若BH=AC,求∠AOC的度数.
(2)如图2延长BE交⊙O于点G,求证:HE=GE;
(3)如图3,在(2)的条件下,P是弦AC上一点,过点P作PM∥BC交AB于点M,若∠PCD+2∠PDC=90°,BM=![]() ,AM=
,AM=![]() ,求⊙O半径.
,求⊙O半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形![]() 中,,
中,,![]() 以边
以边![]() 所在的直线为轴建立平面直角坐标系
所在的直线为轴建立平面直角坐标系![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,点
,点![]() 是
是![]() 轴正半轴上的动点,将点
轴正半轴上的动点,将点![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,使点
,使点![]() 恰好落在反比例
恰好落在反比例![]() 的图象上,则
的图象上,则![]() 的值是__________.
的值是__________.
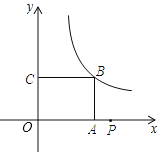
查看答案和解析>>
科目:初中数学 来源: 题型:
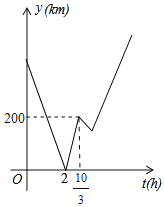
【题目】A,C,B三地依次在一条笔直的道路上甲、乙两车同时分别从A,B两地出发,相向而行.甲车从A地行驶到B地就停止,乙车从B地行驶到A地后,立即以相同的速度返回B地,在整个行驶的过程中,甲、乙两车均保持匀速行驶,甲、乙两车距C地的距离之和y(km)与甲车出发的间(b)之间的函数关系如图所示,则甲车到达B地时,乙车距B地的距离为_____km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,且
,且![]() .
.
(1)若![]() 是第二象限位于直线
是第二象限位于直线![]() 上方的一点,过
上方的一点,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 轴交直线
轴交直线![]() 于
于![]() ,
,![]() 为
为![]() 中点,其中
中点,其中![]() 的周长是
的周长是![]() ,若
,若![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() ,求
,求![]() 的最小值,此时
的最小值,此时![]() 轴上有一个动点
轴上有一个动点![]() ,当
,当![]() 最大时,求
最大时,求![]() 点坐标;
点坐标;
(2)在(1)的情况下,将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 后得到
后得到![]() ,如图2,将线段
,如图2,将线段![]() 沿着
沿着![]() 轴平移,记平移过程中的线段
轴平移,记平移过程中的线段![]() 为
为![]() ,在平面直角坐标系中是否存在点
,在平面直角坐标系中是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形,若存在,请求出点
为顶点的四边形为菱形,若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
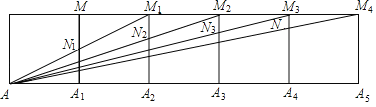
【题目】将2019个边长为1的正方形按如图所示的方式排列,点A,A1,A2,A3…A2019和点M,M1,M2…M2018是正方形的顶点,连接AM1,AM2,AM3…AM2018分别交正方形的边A1M,A2M1,A3M2…A2018M2017于点N1,N2,N3…N2018,四边形M1N1A1A2的面积是S1,四边形M2N2A2A3的面积是S2,…,则S2018为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com