
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,且
,且![]() .
.
(1)若![]() 是第二象限位于直线
是第二象限位于直线![]() 上方的一点,过
上方的一点,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 轴交直线
轴交直线![]() 于
于![]() ,
,![]() 为
为![]() 中点,其中
中点,其中![]() 的周长是
的周长是![]() ,若
,若![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() ,求
,求![]() 的最小值,此时
的最小值,此时![]() 轴上有一个动点
轴上有一个动点![]() ,当
,当![]() 最大时,求
最大时,求![]() 点坐标;
点坐标;
(2)在(1)的情况下,将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 后得到
后得到![]() ,如图2,将线段
,如图2,将线段![]() 沿着
沿着![]() 轴平移,记平移过程中的线段
轴平移,记平移过程中的线段![]() 为
为![]() ,在平面直角坐标系中是否存在点
,在平面直角坐标系中是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形,若存在,请求出点
为顶点的四边形为菱形,若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

【答案】(1)![]() ;
;![]()
(2)存在,![]() 或
或![]() 或
或![]()
【解析】
(1)点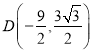 ,则点
,则点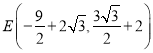 ,过点C作x轴的垂线、过点M作y轴的垂线,两垂线交于点H, MH=MC
,过点C作x轴的垂线、过点M作y轴的垂线,两垂线交于点H, MH=MC![]() =
=![]() MC, 当点E、M、H三点共线时,EM+MH=EM+
MC, 当点E、M、H三点共线时,EM+MH=EM+![]() MC最小, 点M
MC最小, 点M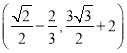 ,连接BM交于y轴于点G,此时
,连接BM交于y轴于点G,此时![]() 最大,即可求解;
最大,即可求解;
(2)设线段![]() 沿着x轴平移了m个单位,则点
沿着x轴平移了m个单位,则点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、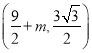 ,而点E
,而点E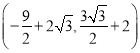 ,
,
①当![]() 是菱形的边时,则EP(
是菱形的边时,则EP(![]() )=
)=![]() =OA=
=OA=![]() ,即可求解;
,即可求解;
②当![]() 是菱形的对角线时,
是菱形的对角线时,
设点P(a,b), 由中点公式得:![]() ,
,![]() ,而EO=EA,即:
,而EO=EA,即:![]() +
+![]() =
=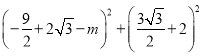 ,即可求解.
,即可求解.
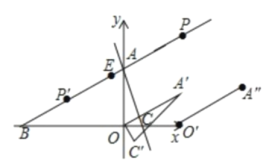
(1)由AC: ![]() 得:点A、C的坐标分别为:
得:点A、C的坐标分别为:![]() 、
、![]() ,
,
∴AO=![]() ,CO=
,CO=![]() ,
,![]() ,
,
则![]() ,则
,则![]() ,
,
点B![]() ,点A
,点A![]() ,代入y=ax+b,
,代入y=ax+b,
得: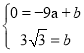 ,解得:
,解得: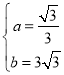 ,
,
则直线AB的表达式为:![]() ,
,
∴BO=9,AO=![]()
∴![]() ,则
,则![]() ,
,![]() ,
,
∵FE![]() AB,FD∥y轴,则
AB,FD∥y轴,则![]() ,
,
设:DE=s,则DF=2s,EF=![]() s,
s, ![]() 的周长是12+
的周长是12+![]() ,解得:s=4,
,解得:s=4,
D为AB的中点,则点 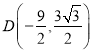 ,
,
s=ED=4,则![]() ,
,
则点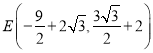 ,
,
过点C作x轴的垂线、过点M作y轴的垂线,两垂线交于点H,如图1:
则![]() ,则MH=MC
,则MH=MC![]() =
=![]() MC,
MC,
当点E、M、H三点共线时,EM+MH=EM+![]() MC最小,
MC最小,
则![]() ,
,
作点M在直线AC上,则点M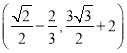 ,
,
作点M关于y轴的对称点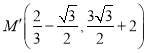 ,连接BM交于y轴于点G,如图2:
,连接BM交于y轴于点G,如图2:
则点G为所求,此时![]() 最大,
最大,
将B![]() 、
、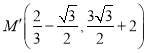 的坐标代入一次函数表达式:
的坐标代入一次函数表达式:![]() ,
,
解得:![]()
故点G的坐标为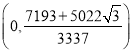 ;
;
综上,EM+![]() MC最小值为:
MC最小值为:![]() , G的坐标为:
, G的坐标为: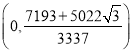 ;
;
(2)将![]() 绕O点顺时针旋转
绕O点顺时针旋转![]() 后得到
后得到![]() ,
,
则![]() 为边长为4的等边三角形,则点
为边长为4的等边三角形,则点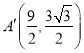 ,
,
设线段![]() 沿着x轴平移了m个单位,
沿着x轴平移了m个单位,
则点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、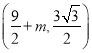 ,而点E
,而点E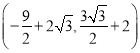 ,
,
①当![]() 是菱形的边时,
是菱形的边时,
直线![]() 和直线AB的倾斜角都是
和直线AB的倾斜角都是![]() ,故
,故![]() ∥
∥![]() ∥AB,
∥AB,
则EP(![]() )=
)=![]() =OA=
=OA=![]() ,
,
则![]() ,
,
故点P![]() ,
,
同理点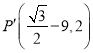 ;
;
②当![]() 是菱形的对角线时,
是菱形的对角线时,
设点P(a,b),
由中点公式得:![]() ,
,![]() ,
,
而EO=EA,即:![]() +
+![]() =
=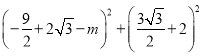 ,
,
解得![]() ,b=-2,
,b=-2,![]() ,
,
故:![]() ,b=-2,
,b=-2,
则点P![]() ;
;
综上,点P坐标为:![]() 或
或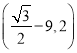 或
或![]() .
.





 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,以点
,以点![]() 为圆心,适当长度为半径作弧,分别交边
为圆心,适当长度为半径作弧,分别交边![]() 于点
于点![]() ,分别以
,分别以![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 内交于点
内交于点![]() ,作射线
,作射线![]() .若
.若![]() 是
是![]() 上一点,过点
上一点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,且
,且![]() ,则直线
,则直线![]() 与
与![]() 之间的距离是( )
之间的距离是( )
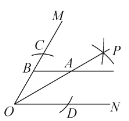
A.![]() B.
B.![]() C.3D.6
C.3D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,半径
中,半径![]() 直径
直径![]() 与
与![]() 相切于点
相切于点![]() 连接
连接![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
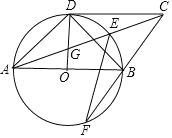
![]() 求证:
求证: ![]() ;
;
![]() 若
若![]()
①求证:四边形![]() 是平行四边形;
是平行四边形;
②连接![]() ,当
,当![]() 的半径为
的半径为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】入学考试前,某语文老师为了了解所任教的甲、乙两班学生假期向的语文基础知识背诵情况,对两个班的学生进行了语文基础知识背诵检测,满分100分.现从两个班分别随机抽取了20名学生的检测成绩进行整理,描述和分析(成绩得分用x表示,共分为五组:
A.0≤x<80,B.80≤x<85,C.85≤x<90,D.90≤x<95,E.95≤x<100),下面给出了部分信息:
甲班20名学生的成绩为:
甲组 | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
乙班20名学生的成绩在D组中的数据是:93,91,92,94,92,92,92
甲、乙两班抽取的学生成绩数据统计表
班级 | 甲组 | 乙组 |
平均数 | 91 | 92 |
中位数 | 91 | b |
众数 | c | 92 |
方差 | 41.2 | 27.3 |
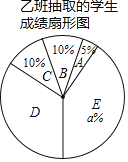
根据以上信息,解答下列问题:
(1)直接写出上述图表中a,b,c的值:a= ;b= ;c= ;
(2)根据以上数据,你认为甲、乙两个班中哪个班的学生基础知识背诵情况较好?请说明理由(一条理由即可);
(3)若甲、乙两班总人数为125,且都参加了此次基础知识检测,估计此次检测成绩优秀(x≥95)的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
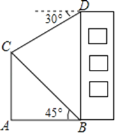
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某飞机场东西方向的地面l上有一长为1 km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5![]() 千米的C处.
千米的C处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
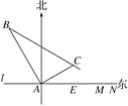
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A.将函数y=![]() x+1向右平移2个单位后所得函数的解析式为y=
x+1向右平移2个单位后所得函数的解析式为y=![]() x
x
B.若一个数的平方根等于其本身,则这个数是0和1
C.对函数y=![]() ,其函数值y随自变量x的增大而增大
,其函数值y随自变量x的增大而增大
D.直线y=3x+1与直线y=﹣3x+2一定互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() 、
、![]() 、
、![]() .
.
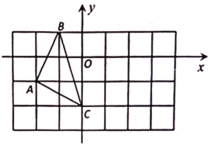
(1)点![]() 关于坐标原点
关于坐标原点![]() 对称的点的坐标为______;
对称的点的坐标为______;
(2)将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后得到的
,画出旋转后得到的![]() ;
;
(3)在(2)中,求边![]() 所扫过区域的面积是多少?(结果保留
所扫过区域的面积是多少?(结果保留![]() ).
).
(4)若![]() 、
、![]() 、
、![]() 三点的横坐标都加3,纵坐标不变,图形
三点的横坐标都加3,纵坐标不变,图形![]() 的位置发生怎样的变化?
的位置发生怎样的变化?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com