
����Ŀ����ѧ����ǰ��ij������ʦΪ���˽����ν̵ļס�������ѧ������������Ļ���֪ʶ������������������ѧ�����������Ļ���֪ʶ���м�⣬����100�֣��ִ�������ֱ������ȡ��20��ѧ���ļ��ɼ����������������ͷ������ɼ��÷���x��ʾ������Ϊ���飺
A.0��x��80��B.80��x��85��C.85��x��90��D.90��x��95��E.95��x��100������������˲�����Ϣ��
�װ�20��ѧ���ijɼ�Ϊ��
���� | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
�Ұ�20��ѧ���ijɼ���D���е������ǣ�93��91��92��94��92��92��92
�ס��������ȡ��ѧ���ɼ�����ͳ�Ʊ�
�༶ | ���� | ���� |
ƽ���� | 91 | 92 |
��� | 91 | b |
���� | c | 92 |
���� | 41.2 | 27.3 |
����������Ϣ������������⣺
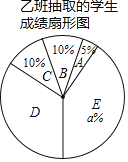
��1��ֱ��д������ͼ����a��b��c��ֵ��a���� ����b���� ����c���� ����
��2�������������ݣ�����Ϊ�ס������������ĸ����ѧ������֪ʶ��������Ϻã���˵�����ɣ�һ�����ɼ��ɣ���
��3�����ס�������������Ϊ125���Ҷ��μ��˴˴λ���֪ʶ��⣬���ƴ˴μ��ɼ����㣨x��95����ѧ�������Ƕ��٣�
���𰸡���1��40��92.5��91����2���Ұ࣬�Ұ��ƽ���֣���λ�������ڼװࣻ��3��44
��������
��1������D���������D����ռ�İٷֱ����![]() ��������λ���������ĸ������
��������λ���������ĸ������![]() ��
��
��2������ƽ��������λ�������ʽ��
��3���������������壬�õ��𰸣�
��1��1��5%��10%��10%��![]() ��40%��
��40%��
��![]() ��40��
��40��
��ͳ�Ʊ��е����ݿ�֪b��![]() ��92.5��
��92.5��
�ɼ�Ϊ91���ڼװ�20��ѧ���ijɼ��г�����4�Σ���࣬��c��91��
�ʴ�Ϊ��40��92.5��91��
��2���Ұ��ѧ������֪ʶ��������Ϻã����ɣ��Ұ��ƽ���֣���λ�������ڼװࣻ
��3���װ�20��ѧ���гɼ����㣨x��95����ѧ�������У�6�ˣ�
�Ұ�20��ѧ���гɼ����㣨x��95����ѧ�������У�![]() �ˣ�
�ˣ�
��125��![]() ��44��
��44��
�𣺹��ƴ˴μ��ɼ����㣨x��95����ѧ��������44�ˣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ε�һ��ƽ����![]() �ᣬһ������
�ᣬһ������![]() ���ϣ����ڵ��⣬���ǵı߳�����Ϊ2��4��6��8����������������
���ϣ����ڵ��⣬���ǵı߳�����Ϊ2��4��6��8����������������![]() ��ʾ������
��ʾ������![]() ��
��![]() �ᡢ�ױ�
�ᡢ�ױ�![]() ��
��![]() ��
��![]() ���������һ����λ����
���������һ����λ����![]() ��������__________��
��������__________��![]() ��������__________��
��������__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
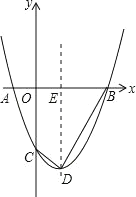
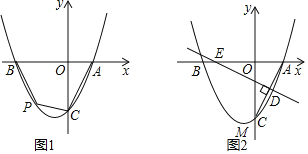
����Ŀ����ͼ����֪��������y��x2+bx+c��x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C����DΪ���㣬����BD��CD�������ߵĶԳ�����x�ύ���E��
��1���������߽���ʽ����D�����ꣻ
��2��G����������B��D֮���һ�㣬��S�ı���CDGB��4S��DGB�����G�����ꣻ
��3������������B��D֮���Ƿ����һ��M������M��MN��CD����ֱ��CD�ڵ�N��ʹ��C��M��NΪ��������������BDE���ƣ������ڣ�������������ĵ�M�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ھ���![]() �У���
�У���![]() �Ա�
�Ա�![]() ���ڵ�ֱ��Ϊ�Ὠ��ƽ��ֱ������ϵ
���ڵ�ֱ��Ϊ�Ὠ��ƽ��ֱ������ϵ![]() ������������
������������![]() ��ͼ����
��ͼ����![]() ����
����![]() ��
��![]() ���������ϵĶ��㣬����
���������ϵĶ��㣬����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ��ʹ��
��ʹ��![]() ǡ�����ڷ�����
ǡ�����ڷ�����![]() ��ͼ���ϣ���
��ͼ���ϣ���![]() ��ֵ��__________��
��ֵ��__________��
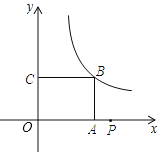
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ�������У�������![]() ����
����![]() ����
����![]() ��ֱ��
��ֱ��![]() �Ϸ��������ϵ�һ���㣬
�Ϸ��������ϵ�һ���㣬![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ��
��
![]() ����������ϵ������������ͼ�����������ߵĺ�������ʽ��
����������ϵ������������ͼ�����������ߵĺ�������ʽ��
![]() ��
��![]() ʱ�����
ʱ�����![]() �����ꣻ
�����ꣻ
![]() ���߶�
���߶�![]() �����ֵ��
�����ֵ��
![]() ���߶�
���߶�![]() ���ʱ������
���ʱ������![]() ��ֱ��
��ֱ��![]() ����
����![]() ��ֱ��д����
��ֱ��д����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��
��1����![]() �ǵڶ�����λ��ֱ��
�ǵڶ�����λ��ֱ��![]() �Ϸ���һ�㣬��
�Ϸ���һ�㣬��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ύֱ��
�ύֱ��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �е㣬����
�е㣬����![]() ���ܳ���
���ܳ���![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ��һ���㣬����
��һ���㣬����![]() ����
����![]() ����Сֵ����ʱ
����Сֵ����ʱ![]() ������һ������
������һ������![]() ����
����![]() ���ʱ����
���ʱ����![]() �����ꣻ
�����ꣻ
��2���ڣ�1��������£���![]() ��
��![]() ��˳ʱ����ת
��˳ʱ����ת![]() ��õ�
��õ�![]() ����ͼ2�����߶�
����ͼ2�����߶�![]() ����
����![]() ��ƽ�ƣ���ƽ�ƹ����е��߶�
��ƽ�ƣ���ƽ�ƹ����е��߶�![]() Ϊ
Ϊ![]() ����ƽ��ֱ������ϵ���Ƿ���ڵ�
����ƽ��ֱ������ϵ���Ƿ���ڵ�![]() ��ʹ���Ե�
��ʹ���Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı���Ϊ���Σ������ڣ��������
Ϊ������ı���Ϊ���Σ������ڣ��������![]() �����꣬�������ڣ���˵�����ɣ�
�����꣬�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ������
������![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
![]() �����������ߵĽ���ʽ��
�����������ߵĽ���ʽ��
![]() ��ͼ1����P�ǵ����������������ϵ�һ�����㣬���ı���
��ͼ1����P�ǵ����������������ϵ�һ�����㣬���ı���![]() ��������ʱ�����
��������ʱ�����![]() �����ꣻ
�����ꣻ
![]() ��ͼ2���߶�
��ͼ2���߶�![]() �Ĵ�ֱƽ���߽�
�Ĵ�ֱƽ���߽�![]() ���ڵ�
���ڵ�![]() ������Ϊ
������Ϊ![]() Ϊ�����ߵĶ��㣬��ֱ��
Ϊ�����ߵĶ��㣬��ֱ��![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ
��ʹ![]() ���ܳ���С�������ڣ������
���ܳ���С�������ڣ������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳����ꡰʮһ���ڼ���й���������������������ĸ���ŷֱ�Ϊ1��2��3��4���ʵأ���С����ͬ��С����������һ��С����С���źŻ����ﲢҡ�ȣ�������һ��С���ټ���С���ţ��̳��涨������������С��֮��Ϊ��8����6��ʱ�����н������ϡ�����ͼ�������б�����������˿�С��μӴ˴������ʱ�н��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶����ʦ��ѧС�龭���г����ˣ��õ�ij���˶�����������y���������ۼ�x��Ԫ/������һ�κ��������ۼۡ���������������������w��Ԫ���������Ӧֵ�����
�ۼ�x��Ԫ/���� | 130 | 150 | 180 |
��������y������ | 210 | 150 | 60 |
����������w��Ԫ�� | 10500 | 10500 | 6000 |
ע�������������������������ۼ۩����ۣ�
��1����y����x�ĺ�������ʽ����Ҫ��д���Ա�����ȡֵ��Χ����
��2���˶����Ľ������� ��Ԫ/����
��3�����ۼ��Ƕ���ʱ�����������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com