
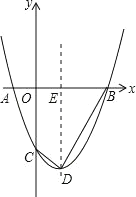
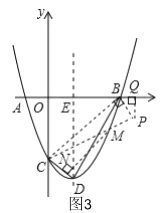
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘЈәЕЧОпПЯyЈҪx2+bx+cУлxЦбҪ»УЪAЈЁ©Ғ1Ј¬0Ј©Ј¬BЈЁ3Ј¬0Ј©БҪөгЈ¬УлyЦбҪ»УЪөгCЈ¬өгDОӘ¶ҘөгЈ¬Б¬ҪУBDЈ¬CDЈ¬ЕЧОпПЯөД¶ФіЖЦбУлxЦбҪ»УлөгEЈ®
ЈЁ1Ј©ЗуЕЧОпПЯҪвОцКҪј°өгDөДЧшұкЈ»
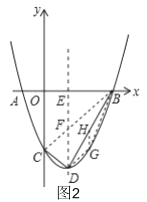
ЈЁ2Ј©GКЗЕЧОпПЯЙПBЈ¬DЦ®јдөДТ»өгЈ¬ЗТSЛДұЯРОCDGBЈҪ4SЎчDGBЈ¬ЗуіцGөгЧшұкЈ»
ЈЁ3Ј©ФЪЕЧОпПЯЙПBЈ¬DЦ®јдКЗ·сҙжФЪТ»өгMЈ¬№эөгMЧчMNЎНCDЈ¬Ҫ»ЦұПЯCDУЪөгNЈ¬К№ТФCЈ¬MЈ¬NОӘ¶ҘөгөДИэҪЗРОУлЎчBDEПаЛЖЈҝИфҙжФЪЈ¬ЗуіцВъЧгМхјюөДөгMөДЧшұкЈ¬ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»¶Ҙөг
Ј»¶Ҙөг![]()
![]() Ј»ЈЁ2Ј©
Ј»ЈЁ2Ј©![]() Ј»ЈЁ3Ј©ҙжФЪЈ¬өг
Ј»ЈЁ3Ј©ҙжФЪЈ¬өг![]() »т
»т![]() Ј®
Ј®
ЎҫҪвОцЎҝ
ЈЁ1Ј©АыУГҙэ¶ЁПөКэ·ЁҝЙЗуөГЕЧОпПЯөДҪвОцКҪЈ¬И»әу»ҜіЙ¶ҘөгКҪҝЙөГөгDөДЧшұкЈ»
ЈЁ2Ј©Б¬ҪУBCЈ¬BGЈ¬DGЈ¬КЧПИЗуіц![]() Ј¬И»әуёщҫЭSЛДұЯРОCDGBЈҪ4SЎчDGBҝЙөГ
Ј¬И»әуёщҫЭSЛДұЯРОCDGBЈҪ4SЎчDGBҝЙөГ![]() Ј¬ЗуіцЦұПЯ
Ј¬ЗуіцЦұПЯ![]() өДҪвОцКҪЈ¬Йи
өДҪвОцКҪЈ¬Йи![]() Ј¬ФтHЈЁxЈ¬2x-6Ј©Ј¬ёщҫЭ
Ј¬ФтHЈЁxЈ¬2x-6Ј©Ј¬ёщҫЭ![]() өГіц·ҪіМЈ¬Ҫв·ҪіМЗуіцxјҙҝЙҪвҫцОКМвЈ»
өГіц·ҪіМЈ¬Ҫв·ҪіМЗуіцxјҙҝЙҪвҫцОКМвЈ»
ЈЁ3Ј©ИзНј3Ј¬ТФCЈ¬MЈ¬NОӘ¶ҘөгөДИэҪЗРОУлЎчBDEПаЛЖЈ¬ФтТФBЈ¬CЈ¬PОӘ¶ҘөгөДИэҪЗРОУлЎчBDEПаЛЖЈ¬Фт![]() »т
»т![]() Ј¬Зуіц
Ј¬Зуіц![]() »т
»т![]() Ј»И»әу·Ц
Ј»И»әу·Ц![]() әН
әН![]() БҪЦЦЗйҝцЈ¬·ЦұрЗуіцЦұПЯCPөДҪвОцКҪјҙҝЙҪвҫцОКМвЈ®
БҪЦЦЗйҝцЈ¬·ЦұрЗуіцЦұПЯCPөДҪвОцКҪјҙҝЙҪвҫцОКМвЈ®
ҪвЈәЈЁ1Ј©![]() ЕЧОпПЯ
ЕЧОпПЯ![]() Ул
Ул![]() ЦбҪ»УЪ
ЦбҪ»УЪ![]() Ј¬
Ј¬![]() БҪөгЈ¬
БҪөгЈ¬
![]() Ј¬ҪвөГ
Ј¬ҪвөГ![]() Ј¬
Ј¬
ЎаЕЧОпПЯөДҪвОцКҪОӘЈә![]() Ј»
Ј»
![]() Ј¬
Ј¬
![]() ¶Ҙөг
¶Ҙөг![]() өДЧшұкОӘ
өДЧшұкОӘ![]() Ј»
Ј»
ЈЁ2Ј©ИзНј2Ј¬Б¬ҪУ![]() Ј¬BGЈ¬DGЈ¬
Ј¬BGЈ¬DGЈ¬
ФЪ![]() ЦРЈ¬Бо
ЦРЈ¬Бо![]() Ј¬Фт
Ј¬Фт![]() Ј¬
Ј¬
Ўаөг![]() Ј¬
Ј¬
ЎаТЧЗуЦұПЯ![]() өДҪвОцКҪОӘ
өДҪвОцКҪОӘ![]() Ј¬
Ј¬
ЙиЦұПЯ![]() Ул¶ФіЖЦбПаҪ»УЪөг
Ул¶ФіЖЦбПаҪ»УЪөг![]() Ј¬
Ј¬
өұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
Ўаөг![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() ЛДұЯРО
ЛДұЯРО![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
Йи№эөг![]() Ул
Ул![]() ЦбЖҪРРөДЦұПЯҪ»BDУЪөг
ЦбЖҪРРөДЦұПЯҪ»BDУЪөг![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ![]() өДҪвОцКҪОӘ
өДҪвОцКҪОӘ![]() Ј¬
Ј¬
Фт![]() Ј¬ҪвөГ
Ј¬ҪвөГ![]() Ј¬
Ј¬
ЎаЦұПЯ![]() өДҪвОцКҪОӘ
өДҪвОцКҪОӘ![]() Ј¬
Ј¬
Йи![]() Ј¬ФтHЈЁxЈ¬2x-6Ј©Ј¬
Ј¬ФтHЈЁxЈ¬2x-6Ј©Ј¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ХыАнөГЈ¬![]() Ј¬
Ј¬
ҪвөГЈә![]() Ј¬Фт
Ј¬Фт![]() Ј¬
Ј¬
Ўаөг![]() Ј»
Ј»
ЈЁ3Ј©ҙжФЪЈ¬
УЙ№ҙ№Й¶ЁАнөГЈ¬![]() Ј¬
Ј¬
ИзНј3Ј¬№эөг![]() Чч
Чч![]() Ҫ»
Ҫ»![]() өДСУіӨПЯУЪ
өДСУіӨПЯУЪ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ул
Ул![]() ЦбөДјРҪЗ¶јКЗ
ЦбөДјРҪЗ¶јКЗ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
УЦ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() ТФ
ТФ![]() Ўў
Ўў![]() Ўў
Ўў![]() ОӘ¶ҘөгөДИэҪЗРОУл
ОӘ¶ҘөгөДИэҪЗРОУл![]() ПаЛЖЈ¬
ПаЛЖЈ¬
![]() ТФ
ТФ![]() Ўў
Ўў![]() Ўў
Ўў![]() ОӘ¶ҘөгөДИэҪЗРОУл
ОӘ¶ҘөгөДИэҪЗРОУл![]() ПаЛЖЈ¬
ПаЛЖЈ¬
![]() »т
»т![]() Ј¬јҙ
Ј¬јҙ![]() »т
»т![]() Ј¬
Ј¬
ҪвөГЈә![]() »т
»т![]() Ј¬
Ј¬
№эөг![]() Чч
Чч![]() ЦбУЪ
ЦбУЪ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
ўЩөұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ўаөг![]() Ј¬
Ј¬
ЙиЦұПЯ![]() өДҪвОцКҪОӘ
өДҪвОцКҪОӘ![]() Ј¬
Ј¬
Фт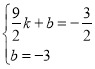 Ј¬ҪвөГ
Ј¬ҪвөГ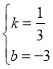 Ј¬
Ј¬
ЎаЦұПЯ![]() өДҪвОцКҪОӘ
өДҪвОцКҪОӘ![]() Ј¬
Ј¬
БӘБў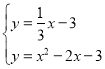 Ј¬ҪвөГЈә
Ј¬ҪвөГЈә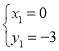 ЈЁЙбИҘЈ©Ј¬
ЈЁЙбИҘЈ©Ј¬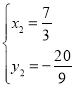 Ј¬
Ј¬
Ўаөг![]() Ј»
Ј»
ўЪөұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ўаөг![]() Ј¬
Ј¬
ЙиЦұПЯ![]() өДҪвОцКҪОӘ
өДҪвОцКҪОӘ![]() Ј¬
Ј¬
Фт![]() Ј¬ҪвөГ
Ј¬ҪвөГ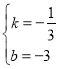 Ј¬
Ј¬
ЎаЦұПЯ![]() өДҪвОцКҪОӘ
өДҪвОцКҪОӘ![]() Ј¬
Ј¬
БӘБў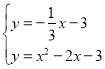 Ј¬ҪвөГ
Ј¬ҪвөГ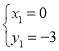 ЈЁЙбИҘЈ©Ј¬
ЈЁЙбИҘЈ©Ј¬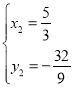 Ј¬
Ј¬
![]() өг
өг![]() Ј¬
Ј¬
ЧЫЙПЛщКцЈ¬ҙжФЪөг![]() »т
»т![]() Ј¬К№ТФ
Ј¬К№ТФ![]() Ўў
Ўў![]() Ўў
Ўў![]() ОӘ¶ҘөгөДИэҪЗРОУл
ОӘ¶ҘөгөДИэҪЗРОУл![]() ПаЛЖЈ®
ПаЛЖЈ®


 »ЖёФ№ЪҫьҝОҝОБ·ПөБРҙр°ё
»ЖёФ№ЪҫьҝОҝОБ·ПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶юҙОәҜКэ![]() өДНјПуИзНјЛщКҫЈ¬ПВБРҪбВЫЈәўЩ
өДНјПуИзНјЛщКҫЈ¬ПВБРҪбВЫЈәўЩ![]() Ј¬ўЪ
Ј¬ўЪ![]() Ј¬ўЫ
Ј¬ўЫ![]() Ј¬ўЬ
Ј¬ўЬ![]() Ј¬ўЭ
Ј¬ўЭ![]() ЈЁmОӘКөКэЈ©Ј¬ХэИ·өДУРЈЁ Ј©
ЈЁmОӘКөКэЈ©Ј¬ХэИ·өДУРЈЁ Ј©
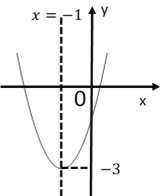
A.1ёцB.2ёцC.3ёцD.4ёц
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
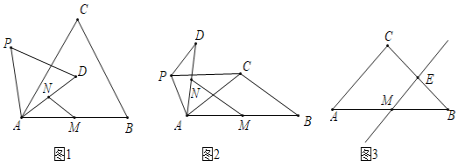
ЎҫМвДҝЎҝФЪЎчABCЦРЈ¬CAЈҪCBЈ¬ЎПACBЈҪҰБЈЁ0ЎгЈјҰБЈј180ЎгЈ©Ј®өгPКЗЖҪГжДЪІ»УлAЈ¬CЦШәПөДИОТвТ»өгЈ¬Б¬ҪУAPЈ¬Ҫ«ПЯ¶ОAPИЖөгPДжКұХлРэЧӘҰБөГөҪПЯ¶ОDPЈ¬Б¬ҪУADЈ¬CPЈ®өгMКЗABөДЦРөгЈ¬өгNКЗADөДЦРөгЈ®
ЈЁ1Ј©ОКМв·ўПЦЈәИзНј1Ј¬өұҰБЈҪ60ЎгКұЈ¬![]() өДЦөКЗЎЎ ЎЎЈ¬ЦұПЯMNУлЦұПЯPCПаҪ»ЛщіЙөДҪПРЎҪЗөД¶ИКэКЗЎЎ ЎЎЈ®
өДЦөКЗЎЎ ЎЎЈ¬ЦұПЯMNУлЦұПЯPCПаҪ»ЛщіЙөДҪПРЎҪЗөД¶ИКэКЗЎЎ ЎЎЈ®
ЈЁ2Ј©АаұИМҪҫҝЈәИзНј2Ј¬өұҰБЈҪ120ЎгКұЈ¬ЗлРҙіцөД![]() Цөј°ЦұПЯMNУлЦұПЯPCПаҪ»ЛщіЙөДҪПРЎҪЗөД¶ИКэЈ¬ІўҫННј2өДЗйРОЛөГчАнУЙЈ®
Цөј°ЦұПЯMNУлЦұПЯPCПаҪ»ЛщіЙөДҪПРЎҪЗөД¶ИКэЈ¬ІўҫННј2өДЗйРОЛөГчАнУЙЈ®
ЈЁ3Ј©ҪвҫцОКМвЈәИзНј3Ј¬өұҰБЈҪ90ЎгКұЈ¬ИфөгEКЗCBөДЦРөгЈ¬өгPФЪЦұПЯMEЙПЈ¬ЗлЦұҪУРҙіцөгBЈ¬PЈ¬DФЪН¬Т»МхЦұПЯЙПКұ![]() өДЦөЈ®
өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪRtЎчABCЦРЈ¬ЎПC = 90ЎгЈ¬өгOКЗРұұЯABЙПТ»¶ЁөгЈ¬өҪөгOөДҫаАлөИУЪOBөДЛщУРөгЧйіЙНјРОWЈ¬НјРОWУлABЈ¬BC·ЦұрҪ»УЪөгDЈ¬EЈ¬Б¬ҪУAEЈ¬DEЈ¬ЎПAED=ЎПBЈ®

ЈЁ1Ј©ЕР¶ПНјРОWУлAEЛщФЪЦұПЯөД№«№ІөгёцКэЈ¬ІўЦӨГчЈ®
ЈЁ2Ј©Иф![]() Ј¬
Ј¬![]() Ј¬ЗуOBЈ®
Ј¬ЗуOBЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјRtЎчABCЦРЈ¬ЎПACBЈҪ90ЎгЈ¬ЎПBЈҪ30ЎгЈ¬ACЈҪ1Ј¬ЗТACФЪЦұПЯlЙПЈ¬Ҫ«ЎчABCИЖөгAЛіКұХлРэЧӘөҪўЩЈ¬ҝЙөГөҪөгP1Ј¬ҙЛКұAP1ЈҪ2Ј»Ҫ«О»ЦГўЩөДИэҪЗРОИЖөгP1ЛіКұХлРэЧӘөҪО»ЦГўЪЈ¬ҝЙөГөҪөгP2Ј¬ҙЛКұAP2ЈҪ2+![]() Ј»Ҫ«О»ЦГўЪөДИэҪЗРОИЖөгP2ЛіКұХлРэЧӘөҪО»ЦГўЫЈ¬ҝЙөГөҪөгP3Ј¬ҙЛКұAP3ЈҪ3+
Ј»Ҫ«О»ЦГўЪөДИэҪЗРОИЖөгP2ЛіКұХлРэЧӘөҪО»ЦГўЫЈ¬ҝЙөГөҪөгP3Ј¬ҙЛКұAP3ЈҪ3+![]() Ј»Ўӯ°ҙҙЛ№жВЙјМРшРэЧӘЈ¬ЦұөҪөгP2020ОӘЦ№Ј¬ФтAP2020өИУЪ_______Ј®
Ј»Ўӯ°ҙҙЛ№жВЙјМРшРэЧӘЈ¬ЦұөҪөгP2020ОӘЦ№Ј¬ФтAP2020өИУЪ_______Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЎчABCЦРЈ¬AB=ACЈ¬BDЎНACУЪDЈ¬ИфcosЎПBAD=![]() Ј¬BD=
Ј¬BD=![]() Ј¬ФтCDөДіӨОӘ__________Ј®
Ј¬ФтCDөДіӨОӘ__________Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПВБРЛө·ЁХэИ·өДКЗЈЁ Ј©
A.ОеХЕНкИ«ПаН¬өДҝЁЖ¬ЙПЈ¬·Цұр»ӯУРФІЎўЖҪРРЛДұЯРОЎўөИұЯИэҪЗРОЎўҪЗЎўПЯ¶ОЈ¬ПЦҙУЦРЛж»ъійИЎТ»ХЕЈ¬ЗЎәГійөҪЦб¶ФіЖНјРОөДёЕВККЗ![]()
B.КВјюЎ°ИОТв»ӯТ»ёц¶аұЯРОЈ¬ЖдНвҪЗәНКЗ![]() ЎұКЗұШИ»КВјю
ЎұКЗұШИ»КВјю
C.Т»ёцәРЧУЦРУР°ЧЗт![]() ёцЈ¬әмЗт
ёцЈ¬әмЗт![]() ёцЈ¬әЪЗт
ёцЈ¬әЪЗт![]() ёц(ГҝёціэБЛСХЙ«Нв¶јПаН¬)Ј®Из№ыҙУЦРИОИЎТ»ёцЗтЈ¬ИЎөГөДКЗәмЗтөДёЕВКУлІ»КЗәмЗтөДёЕВКПаН¬Ј¬ДЗГҙ
ёц(ГҝёціэБЛСХЙ«Нв¶јПаН¬)Ј®Из№ыҙУЦРИОИЎТ»ёцЗтЈ¬ИЎөГөДКЗәмЗтөДёЕВКУлІ»КЗәмЗтөДёЕВКПаН¬Ј¬ДЗГҙ![]() Ул
Ул![]() өДІоКЗ
өДІоКЗ![]()
D.КВјюЎ°°С![]() ёцЗт·ЕИлИэёційМлЦРЈ¬ЖдЦРТ»ёційМлЦРЦБЙЩУР
ёцЗт·ЕИлИэёційМлЦРЈ¬ЖдЦРТ»ёційМлЦРЦБЙЩУР![]() ёцЗтЎұКЗЛж»ъКВјю
ёцЗтЎұКЗЛж»ъКВјю
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИлС§ҝјКФЗ°Ј¬ДіУпОДАПКҰОӘБЛБЛҪвЛщИОҪМөДјЧЎўТТБҪ°аС§ЙъјЩЖЪПтөДУпОД»щҙЎЦӘК¶ұіЛРЗйҝцЈ¬¶ФБҪёц°аөДС§ЙъҪшРРБЛУпОД»щҙЎЦӘК¶ұіЛРјмІвЈ¬Въ·Ц100·ЦЈ®ПЦҙУБҪёц°а·ЦұрЛж»ъійИЎБЛ20ГыС§ЙъөДјмІвіЙјЁҪшРРХыАнЈ¬ГиКцәН·ЦОцЈЁіЙјЁөГ·ЦУГxұнКҫЈ¬№І·ЦОӘОеЧйЈә
A.0ЎЬxЈј80Ј¬B.80ЎЬxЈј85Ј¬C.85ЎЬxЈј90Ј¬D.90ЎЬxЈј95Ј¬E.95ЎЬxЈј100Ј©Ј¬ПВГжёшіцБЛІҝ·ЦРЕПўЈә
јЧ°а20ГыС§ЙъөДіЙјЁОӘЈә
јЧЧй | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
ТТ°а20ГыС§ЙъөДіЙјЁФЪDЧйЦРөДКэҫЭКЗЈә93Ј¬91Ј¬92Ј¬94Ј¬92Ј¬92Ј¬92
јЧЎўТТБҪ°аійИЎөДС§ЙъіЙјЁКэҫЭНіјЖұн
°ај¶ | јЧЧй | ТТЧй |
ЖҪҫщКэ | 91 | 92 |
ЦРО»Кэ | 91 | b |
ЦЪКэ | c | 92 |
·ҪІо | 41.2 | 27.3 |
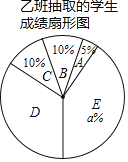
ёщҫЭТФЙПРЕПўЈ¬ҪвҙрПВБРОКМвЈә
ЈЁ1Ј©ЦұҪУРҙіцЙПКцНјұнЦРaЈ¬bЈ¬cөДЦөЈәaЈҪЎЎ ЎЎЈ»bЈҪЎЎ ЎЎЈ»cЈҪЎЎ ЎЎЈ»
ЈЁ2Ј©ёщҫЭТФЙПКэҫЭЈ¬ДгИПОӘјЧЎўТТБҪёц°аЦРДДёц°аөДС§Йъ»щҙЎЦӘК¶ұіЛРЗйҝцҪПәГЈҝЗлЛөГчАнУЙЈЁТ»МхАнУЙјҙҝЙЈ©Ј»
ЈЁ3Ј©ИфјЧЎўТТБҪ°аЧЬИЛКэОӘ125Ј¬ЗТ¶јІОјУБЛҙЛҙО»щҙЎЦӘК¶јмІвЈ¬№АјЖҙЛҙОјмІвіЙјЁУЕРгЈЁxЎЭ95Ј©өДС§ЙъИЛКэКЗ¶аЙЩЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
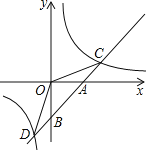
ЎҫМвДҝЎҝИзНјЈ¬ЦұПЯyЈҪkx+bУлxЦбҪ»УЪөгAЈ¬УлyЦбҪ»УЪөгBЈ¬OBЈҪ4Ј¬sinЎПCBOЈҪ![]() Ј®
Ј®
ЈЁ1Ј©ЗуЦұПЯABөДҪвОцКҪЈ»
ЈЁ2Ј©ЦұПЯABУл·ҙұИАэәҜКэyЈҪ![]() ПаҪ»УЪCЎўDБҪөгЈЁCөгФЪөЪТ»ПуПЮЈ©Ј¬ЗуSЎчDOCөДГж»эЈ®
ПаҪ»УЪCЎўDБҪөгЈЁCөгФЪөЪТ»ПуПЮЈ©Ј¬ЗуSЎчDOCөДГж»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com