
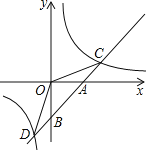
【题目】如图,直线y=kx+b与x轴交于点A,与y轴交于点B,OB=4,sin∠CBO=![]() .
.
(1)求直线AB的解析式;
(2)直线AB与反比例函数y=![]() 相交于C、D两点(C点在第一象限),求S△DOC的面积.
相交于C、D两点(C点在第一象限),求S△DOC的面积.
【答案】(1)直线AB的解析式为y=x﹣4;(2)S△DOC的面积:16.
【解析】
(1)由sin∠CBO=![]() 得出∠CBO=45°,即可得出△AOB是等腰直角三角形,从而求得A、B的坐标,然后根据待定系数法即可求得直线AB的解析式;
得出∠CBO=45°,即可得出△AOB是等腰直角三角形,从而求得A、B的坐标,然后根据待定系数法即可求得直线AB的解析式;
(2)解析式联立求得交点C、D的坐标,然后根据S△DOC=S△BOC+S△BOD即可求得.
解:(1)∵OB=4,sin∠CBO=![]() .
.
∴∠CBO=45°,
∴△AOB是等腰直角三角形,
∴OA=OB=4,
∴A(4,0),B(0,﹣4),
代入y=kx+b得![]() ,
,
解得k=1,b=﹣4,
∴直线AB的解析式为y=x﹣4;
(2)解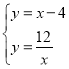
得![]() 或
或![]() ,
,
∴C(6,2),D(﹣2,﹣6),
∴S△DOC=S△BOC+S△BOD=![]() =16.
=16.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,点D为顶点,连接BD,CD,抛物线的对称轴与x轴交与点E.
(1)求抛物线解析式及点D的坐标;
(2)G是抛物线上B,D之间的一点,且S四边形CDGB=4S△DGB,求出G点坐标;
(3)在抛物线上B,D之间是否存在一点M,过点M作MN⊥CD,交直线CD于点N,使以C,M,N为顶点的三角形与△BDE相似?若存在,求出满足条件的点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求这条抛物线的解析式;
求这条抛物线的解析式;
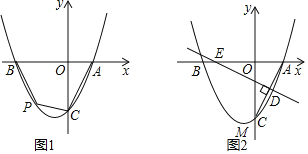
![]() 如图1,点P是第三象限内抛物线上的一个动点,当四边形
如图1,点P是第三象限内抛物线上的一个动点,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 如图2,线段
如图2,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,垂足为
,垂足为![]() 为抛物线的顶点,在直线
为抛物线的顶点,在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年“十一”期间举行购物摸奖活动,摸奖箱里有四个标号分别为1,2,3,4的质地,大小都相同的小球,任意摸出一个小球,记下小球标号后,放回箱里并摇匀,再摸出一个小球,再记下小球标号.商场规定:两次摸出的小球之和为“8”或“6”时才算中奖.请结合“树形图法”或“列表法”,求出顾客小彦参加此次摸奖活动时中奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某一时刻,小宁站在斜坡AC上的A处,小李在大楼FD的楼顶F处,此时小宁望小李的仰角为18.43°.5秒后,小宁沿斜坡AC前进到达C处,小李从大楼F处下楼到大楼E处,此时小李望小宁的俯角为22.6°;然后小李继续下楼,小宁沿CD前往楼底D处,已知小宁的速度为5.2米/秒,大楼FD的高度为30米,斜坡AC的坡度为1:2.4,小李、小宁都保持匀速前进,若斜坡、大楼在同一平面内,小李、小宁的身高忽略不计,则当小李达到楼底D处时,小宁距离D处的距离为( )米.
(已知:tan18.43°≈![]() ,sin18.43°≈
,sin18.43°≈![]() ,cos22.6°≈
,cos22.6°≈![]() ,tan22.6≈
,tan22.6≈![]() )
)

A.10B.15.6C.20.4D.26
查看答案和解析>>
科目:初中数学 来源: 题型:
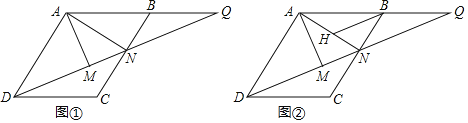
【题目】已知平行四边形ABCD中,N是边BC上一点,延长DN、AB交于点Q,过A作AM⊥DN于点M,连接AN,则AD⊥AN.
(1)如图①,若tan∠ADM=![]() ,MN=3,求BC的长;
,MN=3,求BC的长;
(2)如图②,过点B作BH∥DQ交AN于点H,若AM=CN,求证:DM=BH+NH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某中学为了丰富校园文化生活.校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查。将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:
(1)通过计算补全条形统计图;
(2)在这次调查中,一共抽取了多少名学生?
(3)如果全校有680名学生,请你估计这680名学生中参加演讲比赛的学生有多少名?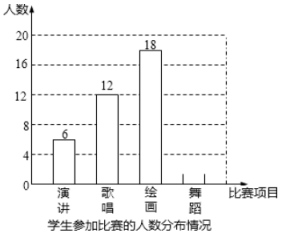
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级孟老师数学小组经过市场调査,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如表:
售价x(元/件) | 130 | 150 | 180 |
月销售量y(件) | 210 | 150 | 60 |
月销售利润w(元) | 10500 | 10500 | 6000 |
注:月销售利润=月销售量×(售价﹣进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)运动服的进价是 元/件;
(3)当售价是多少时,月销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为引导学生广泛阅读文学名著,某校在七年级、八年级开展了读书知识竞赛,该校七、八年级各有学生![]() 人,各随机抽取
人,各随机抽取![]() 名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
七年级:
![]()
八年级:
![]()
成绩人数 |
|
|
|
|
|
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
平均数、中位数、众数如表所示:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
根据以上信息,回答下列问题:
![]()
![]() ,
,![]() ,
,![]() _
_
![]() 该校对读书知识竞赛成绩不少于
该校对读书知识竞赛成绩不少于![]() 分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
![]() 结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由
结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com