
【题目】在△ABC中,AB=AC,BD⊥AC于D,若cos∠BAD=![]() ,BD=
,BD=![]() ,则CD的长为__________.
,则CD的长为__________.
【答案】1或5
【解析】
分两种情况:①若△ABC为锐角三角形,在Rt△ABD中由cos∠BAD=![]() ,可设AD=2x,AB=3x,结合BD的长根据勾股定理列方程,求得x的值后即可得AB=AC=3,AD=2,由CD=ACAD得出答案;②若△ABC为钝角三角形,同理可得AD=2,AB=AC=3,由CD=AC+AD得出答案.
,可设AD=2x,AB=3x,结合BD的长根据勾股定理列方程,求得x的值后即可得AB=AC=3,AD=2,由CD=ACAD得出答案;②若△ABC为钝角三角形,同理可得AD=2,AB=AC=3,由CD=AC+AD得出答案.
解:①如图1,若△ABC为锐角三角形,
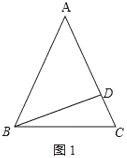
∵BD⊥AC,
∴∠ADB=90°,
∵cos∠BAD=![]() ,
,
∴设AD=2x,AB=3x,
∵AB2=AD2+BD2,
∴9x2=4x2+5,
解得:x=1或x=1(舍),
∴AB=AC=3x=3,AD=2x=2,
∴CD=ACAD=1;
②如图2,若△ABC为钝角三角形,
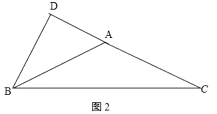
同理可得,AD=2,AB=AC=3,
∴CD=AC+AD=5,
故答案为:1或5.


科目:初中数学 来源: 题型:
【题目】如图,⊙O中,AC为直径,MA,MB分别切⊙O于点A,B,∠BAC=25°,则∠AMB的大小为( )
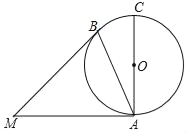
A. 25°B. 30°C. 45°D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解“校园文明监督岗”的值围情况,对全校各班级进行了抽样调查,过程如下:
收集数据:从三个年级中随机抽取了20个班级,学校对各班的评分如下:
92 71 89 82 69 82 96 83 77 83
80 82 66 73 82 78 92 70 74 59
整理、描述数据:按如下分数段整理、描述这两组样本数据:
分数段 |
|
|
|
|
|
班级数 | 1 | 2 | a | 8 | b |
![]() 说明:成绩90分及以上为优秀,
说明:成绩90分及以上为优秀,![]() 分为良好,
分为良好,![]() 分为合格,60分以下为不合格
分为合格,60分以下为不合格![]()
分析数据:样本数据的平均数、中位数、众数、极差如下表,绘制扇形统计图:
平均数 | 中位数 | 众数 | 极差 |
79 | c | 82 | d |
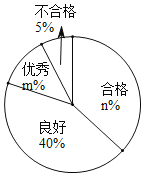
请根据以上信息解答下列问题:
![]() 填空:
填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______.
______.
![]() 若我校共120个班级,估计得分为优秀的班级有多少个?
若我校共120个班级,估计得分为优秀的班级有多少个?
![]() 为调动班级积极性,决定制定一个奖励标准分,凡到达或超过这个标准分的班级都将受到奖励
为调动班级积极性,决定制定一个奖励标准分,凡到达或超过这个标准分的班级都将受到奖励![]() 如果要使得半数左右的班级都能获奖,奖励标准分应定为多少分?并简述其理由
如果要使得半数左右的班级都能获奖,奖励标准分应定为多少分?并简述其理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
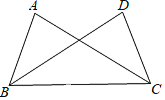
A.∠A=∠DB.∠ACB=∠DBCC.AC=DBD.AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,点D为顶点,连接BD,CD,抛物线的对称轴与x轴交与点E.
(1)求抛物线解析式及点D的坐标;
(2)G是抛物线上B,D之间的一点,且S四边形CDGB=4S△DGB,求出G点坐标;
(3)在抛物线上B,D之间是否存在一点M,过点M作MN⊥CD,交直线CD于点N,使以C,M,N为顶点的三角形与△BDE相似?若存在,求出满足条件的点M的坐标,若不存在,请说明理由.
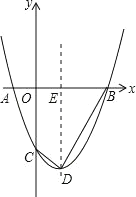
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC内接于⊙O,AD⊥BC于D,BE⊥AC于E,AD、BE交于点H.
(1)如图1,连接OA、OC,若BH=AC,求∠AOC的度数.
(2)如图2延长BE交⊙O于点G,求证:HE=GE;
(3)如图3,在(2)的条件下,P是弦AC上一点,过点P作PM∥BC交AB于点M,若∠PCD+2∠PDC=90°,BM=![]() ,AM=
,AM=![]() ,求⊙O半径.
,求⊙O半径.
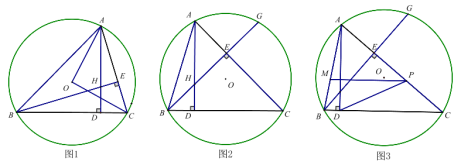
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形![]() 中,,
中,,![]() 以边
以边![]() 所在的直线为轴建立平面直角坐标系
所在的直线为轴建立平面直角坐标系![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,点
,点![]() 是
是![]() 轴正半轴上的动点,将点
轴正半轴上的动点,将点![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,使点
,使点![]() 恰好落在反比例
恰好落在反比例![]() 的图象上,则
的图象上,则![]() 的值是__________.
的值是__________.
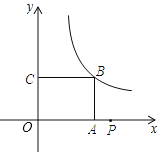
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,且
,且![]() .
.
(1)若![]() 是第二象限位于直线
是第二象限位于直线![]() 上方的一点,过
上方的一点,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 轴交直线
轴交直线![]() 于
于![]() ,
,![]() 为
为![]() 中点,其中
中点,其中![]() 的周长是
的周长是![]() ,若
,若![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() ,求
,求![]() 的最小值,此时
的最小值,此时![]() 轴上有一个动点
轴上有一个动点![]() ,当
,当![]() 最大时,求
最大时,求![]() 点坐标;
点坐标;
(2)在(1)的情况下,将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 后得到
后得到![]() ,如图2,将线段
,如图2,将线段![]() 沿着
沿着![]() 轴平移,记平移过程中的线段
轴平移,记平移过程中的线段![]() 为
为![]() ,在平面直角坐标系中是否存在点
,在平面直角坐标系中是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形,若存在,请求出点
为顶点的四边形为菱形,若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
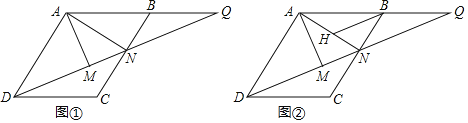
【题目】已知平行四边形ABCD中,N是边BC上一点,延长DN、AB交于点Q,过A作AM⊥DN于点M,连接AN,则AD⊥AN.
(1)如图①,若tan∠ADM=![]() ,MN=3,求BC的长;
,MN=3,求BC的长;
(2)如图②,过点B作BH∥DQ交AN于点H,若AM=CN,求证:DM=BH+NH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com