
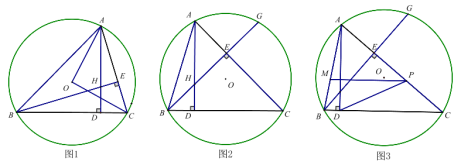
【题目】已知,△ABC内接于⊙O,AD⊥BC于D,BE⊥AC于E,AD、BE交于点H.
(1)如图1,连接OA、OC,若BH=AC,求∠AOC的度数.
(2)如图2延长BE交⊙O于点G,求证:HE=GE;
(3)如图3,在(2)的条件下,P是弦AC上一点,过点P作PM∥BC交AB于点M,若∠PCD+2∠PDC=90°,BM=![]() ,AM=
,AM=![]() ,求⊙O半径.
,求⊙O半径.
【答案】(1)![]() ;(2)答案见解析;(3)5
;(2)答案见解析;(3)5
【解析】
(1)由“AAS”可证△BDH≌△ADC,可得BD=AD,可得∠DBA=∠DAB=45°,由圆周角定理可求∠AOC的度数;
(2)连接AG,证明∠AHG=∠G,可得AH=AG,利用等腰三角形的性质可得HE=GE;
(3)由平行线分线段成比例可求![]() ,通过证明△ADC∽△BAH,可求BH的长,即可求解.
,通过证明△ADC∽△BAH,可求BH的长,即可求解.
解:(1)∵AD⊥BC,BE⊥AC,
∴∠ACD+∠DAC=90°,∠ACD+∠EBC=90°,
∴∠DAC=∠EBC,且∠BDH=∠ADC=90°,BH=AC,
∴△BDH≌△ADC(AAS)
∴BD=AD,且AD⊥BD,
∴∠DBA=∠DAB=45°,
∴∠AOC=2∠ABC=90°;
(2)连接AG,
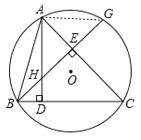
∵∠GAC=∠GBC,且∠GAC+∠G=90°,∠GBC+∠BHD=90°,
∴∠G=∠BHD,
∵∠BHD=∠AHG,
∴∠AHG=∠G,
∴AH=AG,且AC⊥BE,
∴HE=GE;
(3)连接BO并延长交圆O于H,连接AH,
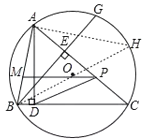
∵PM∥BC,
∴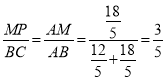 ,
,
∵∠PCD+2∠PDC=90°,
∴∠PCD=90°2∠PDC,
∵∠APD=∠PCD+∠PDC=90°∠PDC,且∠ADP=90°∠PDC,
∴∠APD=∠ADP,
∴AD=AP,
∵PM∥BC,
∴![]() ,
,
∴![]() ,
,
∵BH是直径,
∴∠BAH=90°=∠ADC,且∠H=∠ACB,
∴△ADC∽△BAH,
∴![]() ,
,
∴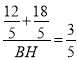 ,
,
∴BH=10,
∴⊙O半径为5.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
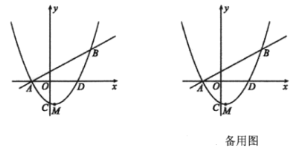
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,抛物线
两点,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() 点,抛物线的顶点为
点,抛物线的顶点为![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 为直线
为直线![]() 下方的抛物线上一动点,当
下方的抛物线上一动点,当![]() 的面积最大时,求
的面积最大时,求![]() 的面积及点
的面积及点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 在抛物线上且位于其对称轴右侧,当
在抛物线上且位于其对称轴右侧,当![]() 与
与![]() 相似时,求
相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,半径
中,半径![]() 直径
直径![]() 与
与![]() 相切于点
相切于点![]() 连接
连接![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
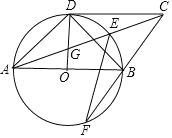
![]() 求证:
求证: ![]() ;
;
![]() 若
若![]()
①求证:四边形![]() 是平行四边形;
是平行四边形;
②连接![]() ,当
,当![]() 的半径为
的半径为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
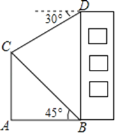
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
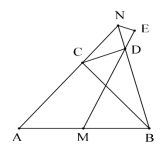
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com