
【题目】如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
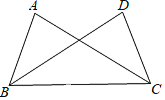
A.∠A=∠DB.∠ACB=∠DBCC.AC=DBD.AB=DC
科目:初中数学 来源: 题型:
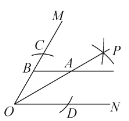
【题目】如图,已知![]() ,以点
,以点![]() 为圆心,适当长度为半径作弧,分别交边
为圆心,适当长度为半径作弧,分别交边![]() 于点
于点![]() ,分别以
,分别以![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 内交于点
内交于点![]() ,作射线
,作射线![]() .若
.若![]() 是
是![]() 上一点,过点
上一点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,且
,且![]() ,则直线
,则直线![]() 与
与![]() 之间的距离是( )
之间的距离是( )
A.![]() B.
B.![]() C.3D.6
C.3D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
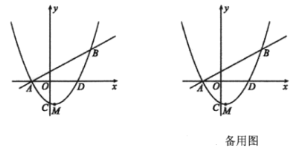
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,抛物线
两点,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() 点,抛物线的顶点为
点,抛物线的顶点为![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 为直线
为直线![]() 下方的抛物线上一动点,当
下方的抛物线上一动点,当![]() 的面积最大时,求
的面积最大时,求![]() 的面积及点
的面积及点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 在抛物线上且位于其对称轴右侧,当
在抛物线上且位于其对称轴右侧,当![]() 与
与![]() 相似时,求
相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W,图形W与AB,BC分别交于点D,E,连接AE,DE,∠AED=∠B.

(1)判断图形W与AE所在直线的公共点个数,并证明.
(2)若![]() ,
,![]() ,求OB.
,求OB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
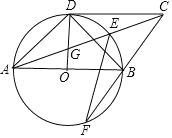
【题目】如图,在![]() 中,半径
中,半径![]() 直径
直径![]() 与
与![]() 相切于点
相切于点![]() 连接
连接![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 求证:
求证: ![]() ;
;
![]() 若
若![]()
①求证:四边形![]() 是平行四边形;
是平行四边形;
②连接![]() ,当
,当![]() 的半径为
的半径为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A.将函数y=![]() x+1向右平移2个单位后所得函数的解析式为y=
x+1向右平移2个单位后所得函数的解析式为y=![]() x
x
B.若一个数的平方根等于其本身,则这个数是0和1
C.对函数y=![]() ,其函数值y随自变量x的增大而增大
,其函数值y随自变量x的增大而增大
D.直线y=3x+1与直线y=﹣3x+2一定互相平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com