
����Ŀ����ƽ��ֱ������ϵxOy�У���P��Q�������ԭ��Գƣ���Ƶ�P���Q��һ������г���������ʾΪ[P��Q]������[P��1��2����Q����1����2��]��һ������г�������
��1��д������������y��![]() ͼ���ϵ�һ������г�������
ͼ���ϵ�һ������г�������
��2����֪���κ���y��x2+mx+n��
�����˺���ͼ���ϴ���һ����г���[A��B]�����е�A������Ϊ��2��4������m��n��ֵ��
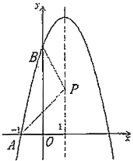
���ڢٵ������£���y����ȡһ��M��0��b��������AMBΪ���ʱ����b��ȡֵ��Χ��
���𰸡���1����ȡ[P��1��1����Q����1����1��]����2����m=2,n=-4����b��ȡֵ��ΧΪ![]() ��
��![]() ��
��
��������
��1������Ŀ��������г��ԵĶ����֪P��Q��Ϊ����ԭ��ԳƵ������㣬�ڷ���������ͼ�����ҳ����㼴�ɣ�
��2������A��BΪ��г��Կ���õ�B�����꣬��ɵõ�����m��n�ķ����飬�������ֵ���ڵ�M��x���Ϸ�ʱ��������á�AMBΪֱ��ʱ��Ӧ��M������꣬����M�����˶�ʱ�����AMBΪ��ǣ�����M��x���·�ʱ��ͬ�������b��ȡֵ��Χ��
�⣺��1����y��![]() ��
��
���ȡ[P��1��1����Q����1����1��]��
��2���١�A��2��4����A��BΪ��г��ԣ�
��B����������2����4����
��A��B�����������y��x2+mx+n���ɵ�![]() ��
��
��![]() ��
��
����ͼ��
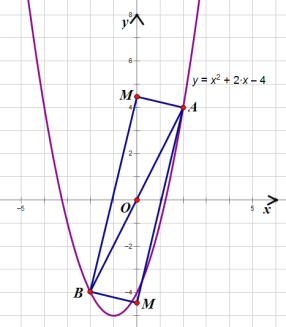
������ M����x���Ϸ�ʱ��
����AMB Ϊֱ�ǣ�M����x���ϣ�������ABCΪֱ�������Σ�
��A��2��4����A��BΪ��г��ԣ�B������Ϊ����2����4����
��ԭ��O��AB�߶�����OΪAB�е㣬
��AB��2OA��
��A��2��4����
��OA��![]() ��
��
��AB��![]() ��
��
��Rt��ABC��
��OΪAB�е�
��MO��OA��![]() ��
��
����AMB Ϊ��ǣ���![]() ��
��
������ M����x���·�ʱ��ͬ���ɵã� ![]() ��
��
����������b��ȡֵ��ΧΪ��![]() ��
��![]() ��
��


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c������A��0����3����B����1��0����C��2����3������������x�����һ����Ϊ��E����PΪ��������һ���㣬���P�ĺ�����Ϊt��
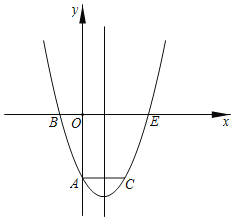
��1���������ߵĽ���ʽ��
��2������P�ڵ�һ���ޣ���MΪ�����߶Գ�����һ�㣬���ı���MBEPǡ����ƽ���ı���ʱ�����P�����ꣻ
��3������P�ڵ������ޣ�����PA��PE��AE����tΪ��ֵʱ����PAE���������������Ƕ��٣�
��4���Ƿ���ڵ�P��ʹ��PAEΪ��AEΪֱ�DZߵ�ֱ�������Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������![]() �ڵ�һ����ͼ����ͼ��ʾ������A��1��0����x��Ĵ��ߣ�������������
�ڵ�һ����ͼ����ͼ��ʾ������A��1��0����x��Ĵ��ߣ�������������![]() ��ͼ���ڵ�M����AOM�����Ϊ3��
��ͼ���ڵ�M����AOM�����Ϊ3��

��1�����������Ľ���ʽ��
��2�����B������Ϊ��t��0��������t��1������ABΪһ�ߵ���������һ�������ڷ���������![]() ��ͼ���ϣ���t��ֵ��
��ͼ���ϣ���t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����4�ſ���ȥ���Ŀ�Ƭ������ֱ�д��1��2��3��4.
(1)һ���������ȡ2�ſ�Ƭ���������ſ�Ƭ�ϵ�����֮��Ϊ�����ĸ��ʣ�
(2)�����ȡ1�źŻز�����һ���������ȡ1�ţ�������ȡ���Ŀ�Ƭ�ϵ�����֮�͵���4�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ������������ÿ�����Ϊ40Ԫ�ĸ��٣���۲��Ź涨ÿ���ۼ۲��ø���55Ԫ���г����鷢�֣���ÿ����45Ԫ�ļ۸����ۣ�ƽ��ÿ������105�䣻ÿ����50Ԫ�ļ۸����ۣ�ƽ��ÿ������90�䣮�ٶ�ÿ��������y���䣩�����ۼ�x��Ԫ/�䣩֮������һ�κ�����ϵʽ��
��1����ƽ��ÿ��������y���䣩�����ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽ��
��2�����������ƽ��ÿ�����������w��Ԫ�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽ��
��3����ÿ��ƻ�������ۼ�Ϊ����Ԫʱ�����Ի�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
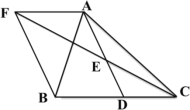
����Ŀ����ͼ������ABC�У�D��BC���ϵ�һ�㣬E��AD���е㣬��A��BC��ƽ���߽�CE���ӳ�����F����AF=BD������BF��
��1����֤��D��BC���е㣻
��2�����AB=AC�����ж��ı���AFBD����״����֤����Ľ��ۡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������һ�����ĸ߶ȣ�����������Ӱ��ǡ�����ڵ����һб���ϣ���ͼ����ʱ��õ����ϵ�Ӱ��Ϊ8���������ϵ�Ӱ��Ϊ4������֪б�µ��½�Ϊ300��ͬһʱ �̣�һ����Ϊl�ס���ֱ�ڵ�������ı���ڵ����ϵ�Ӱ��Ϊ2���������ĸ߶�Ϊ�� ��
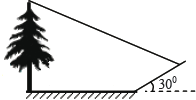
A.![]() �� B.12�� C.
�� B.12�� C.![]() �� D��10��
�� D��10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=60�㣬AC=1��D�DZ�AB���е㣬E�DZ�BC��һ�㣮��DEƽ����ABC���ܳ�����DE�ij���_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ������ϵ�е�λ����ͼ��ʾ������
������ϵ�е�λ����ͼ��ʾ������![]() ��
��![]() ��Ľ���ֱ�Ϊ
��Ľ���ֱ�Ϊ![]() ��
��![]() ��
��![]() ����Գ���
����Գ���![]() �ϵĶ��㣬����ͼ���ṩ����Ϣ���������½��ۣ���
�ϵĶ��㣬����ͼ���ṩ����Ϣ���������½��ۣ���![]() ����
����![]() ��
��![]() ��һ����������
��һ����������![]() ��
��![]() ����
����![]() .������ȷ����______��.
.������ȷ����______��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com