
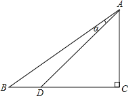
【题目】如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tanB=![]() .
.
(1)求AD的长;
(2)求sinα的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据tanB的值可设AC=3x,则BC=4x,再根据勾股定理求出x,从而求出AC、BC、CD,最后利用勾股定理可求出AD;
(2)过点D作DE⊥AB于E,根据tanB的值可设DE=3y,BE=4y,根据勾股定理求出y,从而求出DE的值,即可求出sinα的值.
解:(1)∵在Rt△ABC中,∠C=90°,tanB=![]()
∴tanB=![]() =
=![]()
设AC=3x,则BC=4x
根据勾股定理:AC2+BC2=AB2
∴(3x)2+(4x)2=52
解得:x=1
∴AC=3,BC=4
∴DC=BC-BD=3
根据勾股定理可得:AD=![]() ;
;
(2)过点D作DE⊥AB于E,如下图所示
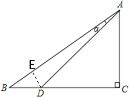
在Rt△BDE中,tanB=![]() =
=![]()
设DE=3y,BE=4y
根据勾股定理:DE2+BE2=BD2
∴(3y)2+(4y)2=12
解得:y=![]()
∴DE=![]() ,BE=
,BE=![]()
∴sinα=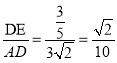


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
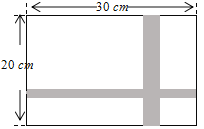
【题目】如图,要设计一副宽20 cm、长30 cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2∶3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
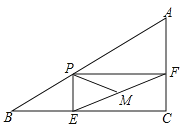
【题目】在Rt△ABC中,∠C=90°,AB=5,AC=3,点P为边AB上一动点(且点P不与点A,B重合),PE⊥BC于E,PF⊥AC于F,点M为EF中点,则PM的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
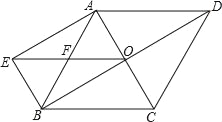
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求:菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
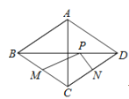
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图: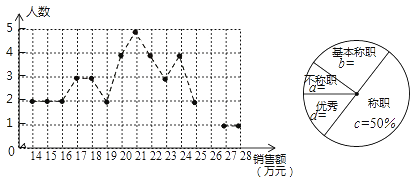
设销售员的月销售额为x(单位:万元)。销售部规定:当x<16时,为“不称职”,当 ![]() 时为“基本称职”,当
时为“基本称职”,当![]() 时为“称职”,当
时为“称职”,当![]() 时为“优秀”.根据以上信息,解答下列问题:
时为“优秀”.根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() :
:![]() 与抛物线
与抛物线![]() :
:![]() 中,若
中,若![]() ,则称抛物线
,则称抛物线![]() ,
,![]() 为“窗帘”抛物线.
为“窗帘”抛物线.
(1)已知![]() 与
与![]() 是“窗帘”抛物线,
是“窗帘”抛物线,
①![]() 的值为______;
的值为______;
②在如图的坐标系中画出它们的大致图像,并直接写出它们的交点坐标.
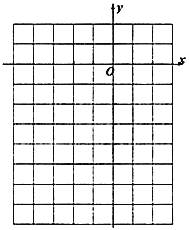
(2)设抛物线![]() ,
,![]() ,
,![]()
![]() 的顶点分别为
的顶点分别为![]() ,
,![]() ,
,![]() ,
,
①判断它们是否是“窗帘”抛物线?答:______(填“是”或“不是”)
②若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com