练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，A、B是双曲线上的点，点A的坐标是是线段AC的中点．

    求k的值；

    求点B的坐标；

    求的面积．

    【答案】（1）4；（2）6.

    【解析】试题分析：（1）把A的坐标代入，即可求得k的值；

    （2）根据A的坐标求得B的纵坐标为2，代入求得x=2，即可求得B的坐标；

    （3）根据A、B的坐标求得直线AB的解析式，求得C的坐标，然后根据三角形面积公式即可求得．

    试题解析：解：（1）把A（1，4）代入，得：4=，解得：k=4；

    （2）由B是AC的中点可得B点的纵坐标是A点纵坐标的一半，即y=2，把y=2代入求得x=2，故B点的坐标为（2，2）；

    （3）由A、B点的坐标求得直线AB的解析式为y=﹣2x+6，令y=0，求得x=3，∴C点的坐标为（3，0），∴△OAC的面积为×3×4=6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某一中学位于东西方向的一条路上，一天我们学校的李老师出校门去家访，他先向东走100米到聪聪家,再向西走150米到青青家,再向东走200米到刚刚家,请问:

    【1】聪聪家与刚刚家相距多远?

    【2】如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出他们家与学校的大概位置(数轴上50米表示单位1).

    【3】聪聪家向西210米所表示的数是多少?

    【4】你认为可用什么办法求数轴上两点之间的距离?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

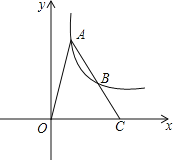
    【题目】某人用如下方法测一钢管的内径：将一小段钢管竖直放在平台上．向内放入两个半径为5 cm的钢球，测得上面一个钢球的最高点到底面的距离DC＝16 cm(钢管的轴截面如图所示)，则钢管的内径AD的长为_______cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB=20，

    （1）写出数轴上点B表示的数　 　；

    （2）|5﹣3|表示5与3之差的绝对值，实际上也可理解为5与3两数在数轴上所对的两点之间的距离．如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离．试探索：

    ①：若|x﹣8|=2，则x=　 　．

    ②：|x+12|+|x﹣8|的最小值为　 　．

    （3）动点P从O点出发，以每秒5个单位长度的速度沿数轴向右匀速运动，设运动时间为t（t＞0）秒．求当t为多少秒时？A，P两点之间的距离为2；

    （4）动点P，Q分别从O，B两点，同时出发，点P以每秒5个单位长度沿数轴向右匀速运动，Q点以P点速度的两倍，沿数轴向右匀速运动，设运动时间为t（t＞0）秒．问当t为多少秒时？P，Q之间的距离为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

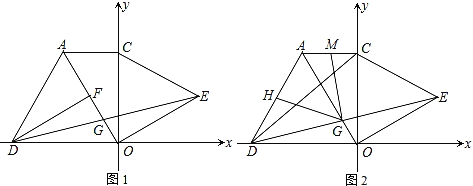
    【题目】如图，在平面直角坐标系中，∠ACO＝90°，∠AOC＝30°，分别以AO、CO为边向外作等边三角形△AOD和等边三角形△COE，DF⊥AO于F，连DE交AO于G．

    （1）求证：△DFG≌△EOG；

    （2）H为AD的中点，连HG，求证：CD＝2HG；

    （3）在（2）的条件下，AC＝4，若M为AC的中点，求MG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有30箱苹果，以每箱20千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：

    与标准质质量的差

    （单位：千克）

    1

    2

    箱数

    2

    6

    10

    8

    4

    （1）这30箱苹果中，最重的一箱比最轻的一箱重多少千克？

    （2）与标准质量比较，这30箱苹果总计超过或不足多少千克？

    （3）若苹果每千克售价6元，则出售这30箱苹果可卖多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某汽车销售公司4月份销售某厂家的汽车，在一定范围内每部汽车的进价与销售量有如下关系；若当月仅售出1辆汽车，则该部汽车的进价为25万元，每多售出1辆，所有售出的汽车的进价均降低0.2万元/辆，月底厂家根据销售量一次性返利给销售公司，销售量在10辆以内（含10辆），每辆返利0.6万元；销售量在10辆以上，每辆返利1.2万元．

    （1）若该公司当月售出3辆汽车，则每辆汽车的进价为________万元；

    （2）若该公司当月售出5辆汽车，且每辆汽车售价为元，则该销售公司该月盈利________万元（用含的代数式表示）．

    （3）如果汽车的售价为25.6万元/辆，该公司计划当月盈利16.8万元，那么需要售出多少辆汽车？（盈利销售利润+返利）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：直线与x轴、y轴分别相交于点A和点B，点C在线段AO上.将沿BC折叠后，点O恰好落在AB边上点D处．

    （1）求出OC的长？

    （2）点E、F是直线BC上的两点，若是以EF为斜边的等腰直角三角形，求点F的坐标；

    （3）取AB的中点M，若点P在y轴上，点Q在直线AB上，是否存在以C、M、P、Q为顶点的四边形为平行四边形？若存在，请求出所有满足条件的Q点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在线段AB上有一点C（点C不与A、B重合且AC＞BC），分别以AC、BC为边作正方形ACED和正方形BCFG，其中点F在边CE上，连接AG．

    （1）如图1，若AC=7，BC=5，则AG=______；

    （2）如图2，若点C是线段AB的三等分点，连接AE、EG，求证：△AEG是直角三角形．

    查看答案和解析>>

    同步练习册答案