
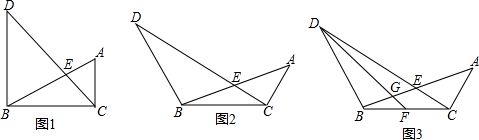
分析 (1)如图1,易证△DEB∽△CEA,然后只需运用相似三角形的性质就可解决问题;
(2)①过点B作BH⊥DC于H,如图2.根据等腰三角形的性质可得∠D=∠BCD=30°,DH=CH,从而可得BH=AC,∠BHE=∠ACE,进而可得△BHE≌△ACE,则有HE=CE,即可证到DE=3EC;②延长DF到点N,使得FN=DF,连接NB、NC,如图3,易证四边形DCNB是平行四边形,从而可得DC∥BN,DC=BN,即可得到△DGE∽△NGB,$\frac{DE}{BN}$=$\frac{3EC}{4EC}$=$\frac{3}{4}$,从而可得$\frac{DG}{NG}$=$\frac{DE}{NB}$=$\frac{3}{4}$.设DG=3k,则有NG=4k,DN=7k,DF=$\frac{1}{2}$DN=$\frac{7k}{2}$,GF=$\frac{k}{2}$,就可得到$\frac{DG}{GF}$的值.
解答 解:(1)如图1,
∵∠ACB=90°,∠DBC=∠ACB,
∴∠DBC=90°,
∴∠DBC+∠ACB=180°,
∴DB∥AC,
∴△DEB∽△CEA,
∴$\frac{DE}{EC}$=$\frac{DB}{CA}$.
∵BD=BC=2AC,
∴DE=2EC;
(2)猜想:DE=3CE.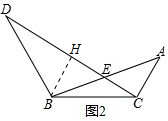
证明:过点B作BH⊥DC于H,如图2.
又∵BD=BC,∠DBC=∠ACB=120°,
∴∠D=∠BCD=30°,DH=CH,
∴DB=2BH,∠ACE=90°,
∴BH=AC,∠BHE=∠ACE.
在△BHE和△ACE中,
$\left\{\begin{array}{l}{∠BHE=∠ACE}\\{∠BEH=∠AEC}\\{BH=AC}\end{array}\right.$,
∴△BHE≌△ACE,
∴HE=CE,
∴DH=HC=2EC,
∴DE=DH+HE=2EC+EC=3EC;
(3)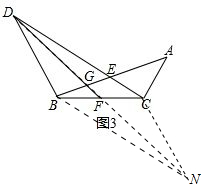 延长DF到点N,使得FN=DF,连接NB、NC,如图3,
延长DF到点N,使得FN=DF,连接NB、NC,如图3,
∵BF=CF,FN=DF,
∴四边形DCNB是平行四边形,
∴DC∥BN,DC=BN,
∴△DGE∽△NGB,$\frac{DE}{BN}$=$\frac{3EC}{4EC}$=$\frac{3}{4}$,
∴$\frac{DG}{NG}$=$\frac{DE}{NB}$=$\frac{3}{4}$.
设DG=3k,则有NG=4k,DN=7k,
∴DF=$\frac{1}{2}$DN=$\frac{7k}{2}$,
∴GF=DF-DG=$\frac{7k}{2}$-3k=$\frac{k}{2}$,
∴$\frac{DG}{GF}$=$\frac{3k}{\frac{k}{2}}$=6.
点评 本题主要考查了相似三角形的判定与性质、全等三角形的判定与性质、平行四边形的判定与性质、等腰三角形的性质、平行线的判定与性质、30°角所对的直角边等于斜边的一半等知识,倍长中线构造平行四边形是解决(2)②小题的关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
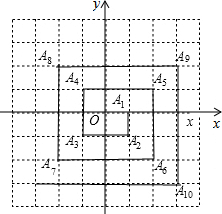 如图,已知A1(1,0),A2(1,1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2010的坐标是( )
如图,已知A1(1,0),A2(1,1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2010的坐标是( )| A. | (502,502) | B. | (-501,-501) | C. | (503,-503) | D. | (-501,501) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
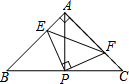 如图,在Rt△ABC中,∠BAC=90°,AB=AC,直角∠EPF的顶点P是BC的中点,将∠EPF绕顶点P旋转,两边PE,PF分别交AB,AC于点E,F.下列四个结论:
如图,在Rt△ABC中,∠BAC=90°,AB=AC,直角∠EPF的顶点P是BC的中点,将∠EPF绕顶点P旋转,两边PE,PF分别交AB,AC于点E,F.下列四个结论:| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
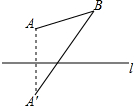 如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )
如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )| A. | A′B2-AB2=13 | B. | A′B2-AB2=24 | C. | A′B2+AB2=25 | D. | A′B2+AB2=26 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BC=CD=20m.
“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BC=CD=20m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com