
����Ŀ��һ���ͳ��Ӽؿ����ҵأ�һ��������ҵؿ����أ�����ͬʱ��������ͳ���صľ���Ϊ![]() ǧ�ף������صľ���Ϊ
ǧ�ף������صľ���Ϊ![]() ǧ�ף�������ʻ��ʱ��ΪxСʱ��
ǧ�ף�������ʻ��ʱ��ΪxСʱ��![]() ��
��![]() ����x��ͼ����ͼ��ʾ��
����x��ͼ����ͼ��ʾ��

��1������ͼ�ֱ�д��![]() ��
��![]() ����x�Ĺ�ϵʽ����Ҫд���Ա���ȡֵ��Χ����
����x�Ĺ�ϵʽ����Ҫд���Ա���ȡֵ��Χ����
��2������������ʱ����x��ֵ��
��3���ס������ؼ���![]() ��
��![]() ��������վ�����200ǧ�ף����ͳ�����
��������վ�����200ǧ�ף����ͳ�����![]() ����վʱ�����ǡ�ý���
����վʱ�����ǡ�ý���![]() ����վ����
����վ����![]() ����վ��صľ��룮
����վ��صľ��룮
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ����3��
����3��![]() ����վ���ؾ���Ϊ
����վ���ؾ���Ϊ![]() ��
��![]() ��
��
��������
��1�����ݴ���ϵ�����������һ�κ�������ʽ��
��2���ⷽ�̼��ɵó������Ȼ���ٷ�����������ۣ�
��3����A����վ�ڼ���B����վ֮�䣬B����վ�ڼ���A����վ֮����������г�������⼴�ɣ�
�⣺��1����![]() ����ͼ��֪������ͼ����
����ͼ��֪������ͼ����![]() ��
��
![]() ��
��
��ã�![]() ��
��
![]() ��
��
��![]() ����ͼ��֪������ͼ����
����ͼ��֪������ͼ����![]() ��
��![]() ����
����
 ��
��
��ã�![]() ��
��
![]() ��
��
��2�������⣬��
![]()
![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
�� ��
��
��3�������⣬��
�ٵ�![]() ����վ�ڼ���
����վ�ڼ���![]() ����վ֮��ʱ��
����վ֮��ʱ��![]() ��
��
���![]() ��
��
��ʱ��![]() ����վ����أ�
����վ����أ�![]() ��
��
�ڵ�![]() ����վ�ڼ���
����վ�ڼ���![]() ����վ֮��ʱ��
����վ֮��ʱ��![]() ��
��
���![]() ����ʱ��
����ʱ��![]() ����վ����أ�
����վ����أ�![]() ��
��
����������![]() ����վ���ؾ���Ϊ
����վ���ؾ���Ϊ![]() ��
��![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֤�������������ڽǵĺ͵���180����
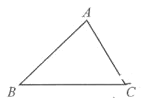
��2���Ķ����ϲ��ش����⣺
��ͼ������ABC��һ��BC�ӳ����õ���ACD���������������ε�һ������һ�ߵ��ӳ�����ɵĽǣ����������ε������������ÿ�����㴦ȡ��������ε�һ����ǣ����ǵĺͽ�����������ε�����Ǻ�������ȫͼ�β�����ABC������Ǻ�����
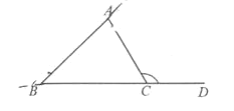
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=![]() �����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ
�����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ![]() ����EB��ED����S��APD+S��APB=1+
����EB��ED����S��APD+S��APB=1+![]() ����S������ABCD=4+
����S������ABCD=4+![]() ��������ȷ���۵�����ǣ� ��
��������ȷ���۵�����ǣ� ��

A.�٢ۢ� B���٢ڢ� C���ۢܢ� D���٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=5��BC=6��ADΪBC���ϵĸߣ�����A��AE��BC������D��DE��AC��AE��DE���ڵ�E��AB��DE���ڵ�F������BE�����ı���AEBD�����
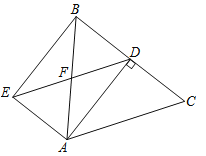
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���P�ǶԽ���BD���е㣬��E��F�ֱ���AB��CD���е㣬AD��BC���ҡ�A+��ABC��90�㣬���PEF��_____��
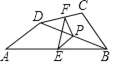
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ж���ʽ�ֽ���ʽ
��1�� 8a3b2-12ab3c ��2��2x3��4x2��2x ��3��![]() ��4����ab+a��+��b+1�� ��5��
��4����ab+a��+��b+1�� ��5��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ŀ��ij�߲��������������½ϵ�ʱ,��װ�к���ϵͳ�Ĵ�������һ������Ȼ�������¶�Ϊ20��������������������Ʒ��.ͼʾ��ij�����ϵͳ�ӿ������رռ��رպ�,�������¶�y(��)��ʱ��x(Сʱ)�仯�ĺ���ͼ��,����BC���Ƿ���������y=һ��ͼ����һ����,�����ͼ����Ϣ�����������
(1)����ϵͳ�����챣�ִ������¶�20����ʱ���ж���Сʱ?
(2)��k��ֵ��
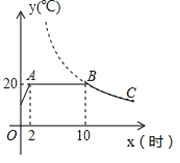
(3)��x=20ʱ,�����ڵ��¶�ԼΪ���ٶ�?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=![]() x2+bx+c������B��3��0����C��0����2����ֱ��L��y=��
x2+bx+c������B��3��0����C��0����2����ֱ��L��y=��![]() x��
x��![]() ��y���ڵ�E�����������߽���A��D���㣬PΪ��������һ���㣨����A��D�غϣ���
��y���ڵ�E�����������߽���A��D���㣬PΪ��������һ���㣨����A��D�غϣ���
��1���������ߵĽ���ʽ��
��2������P��ֱ��L�·�ʱ������P��PN��y�ύL�ڵ�N����PN�����ֵ��
��3������P��ֱ��L�·�ʱ������P��PM��x�ύL�ڵ�M����PM�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() �ֱ���
�ֱ���![]() �ı�
�ı�![]() ���˶��������
���˶��������![]() �غϣ���
�غϣ���![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�![]() ���ӳ��߽���
���ӳ��߽���![]() ��ƽ�����ڵ�
��ƽ�����ڵ�![]() .
.

��1����![]() ����
����![]() �Ķ���.
�Ķ���.
��2����![]() ����
����![]() �Ķ���.
�Ķ���.
��3����![]() �����ú�
�����ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com