
【题目】(1)求证:三角形三个内角的和等于180°.
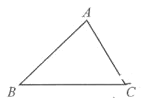
(2)阅读材料并回答问题:
如图,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的“外角”,在每个顶点处取这个三角形的一个外角,它们的和叫做这个三角形的“外角和”.补全图形并求△ABC的“外角和”.
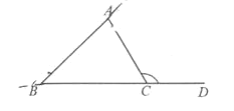
【答案】(1)详见解析;(2)详见解析
【解析】
(1)过A点作MN∥BC,根据平行线的性质及平角的定义解答.
(2)结合三角形的内角和与平角的定义求解即可.
(1)过A点作MN∥BC,
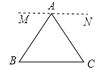
∴∠MAB=∠B,∠NAC=∠C (同位角相等)
∵∠MAB+∠BAC+∠NAC=180°
∴∠B+∠BAC+∠C=180°
∴三角形的内角和为180°
(2)如图:
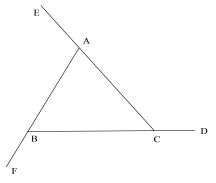
∵∠ACD+∠ACB=180°,∠EAF+∠BAC=180°,∠FBC+∠ABC=180°
∴∠ACD+∠ACB+∠EAF+∠BAC+∠FBC+∠ABC=540°
∵∠ABC+∠BAC+∠ACB=180°
∴∠ACD+∠EAF+∠FBC=360°
即三角形的外角和等于360°


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
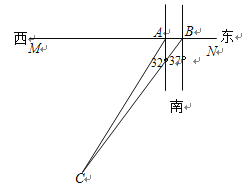
【题目】如图,MN是一条东西方向的海岸线,在海岸线上的A处测得一海岛在南偏西32°的方向上,向东走过780米后到达B处,测得海岛在南偏西37°的方向,求小岛到海岸线的距离.
(参考数据:tan37°= cot53°≈0.755,cot37°= tan53°≈1.327,tan32°= cot58°≈0.625,cot32°= tan58°≈1.600.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月3日至2019年2月20日,“第一届”成都金沙太阳节在金沙遗址博物馆成功举办,用世界文明展览,主题灯展,园林花艺,美食演绎等一系列文化活动,与玛雅这一著名的中美洲文明结下不解之缘,为成都人打造了一个博物馆里的“文化年”.春节当天,小杰于下午![]() 点乘车从家出发,当天按原路返回.如图,是小杰出行的过程中,他距家的距离
点乘车从家出发,当天按原路返回.如图,是小杰出行的过程中,他距家的距离![]() (千米)与他离家的时间
(千米)与他离家的时间![]() (小时)之间的图像.根据图像,完成下面的问题:
(小时)之间的图像.根据图像,完成下面的问题:

(1)小杰家距金沙遗址博物馆 千米,他乘车去金沙遗址博物馆的速度是 千米/小时;
(2)已知晚上![]() 点时,小杰距家
点时,小杰距家![]() 千米,请通过计算说明他何时才能回到家?
千米,请通过计算说明他何时才能回到家?
(3)请直接写出小杰回家过程中![]() 与
与![]() 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(【材料阅读】阅读下列一段文字,然后回答下列问题.
已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:
MN=![]() .
.
例如:已知P(3,1)、Q(1,﹣2),则这两点间的距离PQ=![]() =
=![]() .
.
【直接应用】
(1)已知A(2,-3)、B(-4,5),试求A、B两点间的距离;
(2)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.
【深度应用】
(3)如图,在平面直角坐标系xOy中,二次函数y=x2﹣4的图象与x轴相交于两点A、B,(点A在点B的左边)
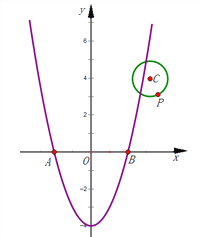
①求点A、B的坐标;
②设点P(m,n)是以点C(3,4)为圆心、1为半径的圆上一动点,求PA2+PB2的最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,DE、BC的延长线相交于点F,且![]() .
.
(1)求证![]() ;
;
(2)当AB=12,AC=9,AE=8时,求BD的长与![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(模型建立)
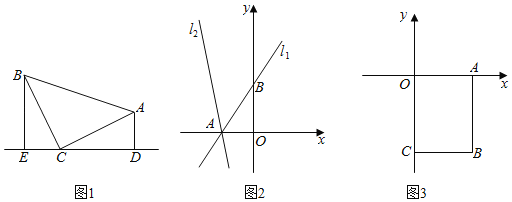
(1)如图1,等腰Rt△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,求证:△BEC≌△CDA;
(模型应用)
(2)如图2,已知直线l1:y=![]() x+3与x轴交于点A,与y轴交于点B,将直线l1绕点A逆时针旋转45°至直线l2;求直线l2的函数表达式;
x+3与x轴交于点A,与y轴交于点B,将直线l1绕点A逆时针旋转45°至直线l2;求直线l2的函数表达式;
(3)如图3,平面直角坐标系内有一点B(3,﹣4),过点B作BA⊥x轴于点A、BC⊥y轴于点C,点P是线段AB上的动点,点D是直线y=﹣2x+1上的动点且在第四象限内.试探究△CPD能否成为等腰直角三角形?若能,求出点D的坐标,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
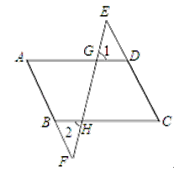
【题目】如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD∥BC和AB∥CD.
请完成下面的推理过程,并填空(理由或数学式):
∵∠1=∠2( )
∠1=∠AGH( )
∴∠2=∠AGH( )
∴AD∥BC( )
∴∠ADE=∠C( )
∵∠A=∠C( )
∴∠ADE=∠A
∴AB∥CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为![]() 千米,出租车离甲地的距离为
千米,出租车离甲地的距离为![]() 千米,两车行驶的时间为x小时,
千米,两车行驶的时间为x小时,![]() 、
、![]() 关于x的图象如图所示:
关于x的图象如图所示:

(1)根据图象,分别写出![]() 、
、![]() 关于x的关系式(需要写出自变量取值范围);
关于x的关系式(需要写出自变量取值范围);
(2)当两车相遇时,求x的值;
(3)甲、乙两地间有![]() 、
、![]() 两个加油站,相距200千米,若客车进入
两个加油站,相距200千米,若客车进入![]() 加油站时,出租车恰好进入
加油站时,出租车恰好进入![]() 加油站,求
加油站,求![]() 加油站离甲地的距离.
加油站离甲地的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com