
【题目】阅读下面材料:小科遇到这样一个问题:如图1,△ABC是等边三角形,点P是三角形内部一点,且PA=3,PB=4,PC=5,求∠APB的度数.
小科是这样思考的:如图2,将AP绕着点A逆时针旋转60°得到AP′,连接P′C,P′P,可以根据边角边证明△APB≌△AP′C,进而通过判定得到两个特殊的三角形,解决问题.
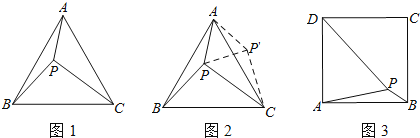
(1)小科遇到的问题中,∠APB的度数是 ;(请直接写出答案)
参考小科同学的思路,解决下列问题:
(2)如图3,在正方形ABCD内有一点P,且PA=2![]() ,PB=2,PD=2
,PB=2,PD=2![]() ,
,
①求∠APB的度数;②求正方形的边长
【答案】(1)150°;(2)①135°;②![]() .
.
【解析】
(1)把△APB绕点A逆时针旋转60°得到△ACP′,由旋转的性质可得P′A=PA,P′C=PB,∠PAP′=60°,证出△APP′是等边三角形,由等边三角形的性质求出PP′=PA=3,∠AP′P=60°,再由勾股定理逆定理求出∠PP′C=90°,求出∠AP′C,即为∠APB的度数;
(2)①把△APB绕点A逆时针旋转90°得到△ADP′,由旋转的性质可得P′A=PA,P′D=PB,∠PAP′=90°,证出△APP′是等腰直角三角形,由等腰直角三角形的性质求出PP′,∠AP′P=45°,再利用勾股定理逆定理求出∠PP′D=90°,然后求出∠AP′D,即为∠APB的度数;
②求出点P′、P、B三点共线,过点A作AE⊥PP′于E,根据等腰直角三角形的性质求出AE=PE=![]() PP′,然后求出BE,在Rt△ABE中,利用勾股定理求出AB即可.
PP′,然后求出BE,在Rt△ABE中,利用勾股定理求出AB即可.
解:(1)如图2,把△APB绕点A逆时针旋转60°得到△ACP′,
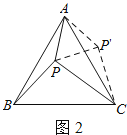
由旋转的性质,P′A=PA=3,P′D=PB=4,∠PAP′=60°,∠APB=∠AP′C,
∴△APP′是等边三角形,
∴PP′=PA=3,∠AP′P=60°,
∵PP′2+P′C2=32+42=25,PC2=52=25,
∴PP′2+P′C2=PC2,
∴∠PP′C=90°,
∴∠AP′C=∠AP′P+∠PP′C=60°+90°=150°;
故∠APB=∠AP′C=150°;
故答案为:150°.
(2)①如图3,把△APB绕点A逆时针旋转90°得到△ADP′,
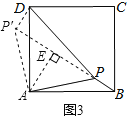
由旋转的性质,P′A=PA=2![]() ,P′D=PB=2,∠PAP′=90°,
,P′D=PB=2,∠PAP′=90°,
∴△APP′是等腰直角三角形,
∴PP′=![]() PA=4,∠AP′P=45°,
PA=4,∠AP′P=45°,
∵PP′2+P′D2=42+22=20,PD2=![]() ,
,
∴PP′2+P′D2=PD2,
∴∠PP′D=90°,
∴∠AP′D=∠AP′P+∠PP′D=45°+90°=135°,
故∠APB=∠AP′D=135°,
②∵∠APB+∠APP′=135°+45°=180°,
∴点P′、P、B三点共线,
过点A作AE⊥PP′于E,
则AE=PE=![]() PP′=
PP′=![]() ×4=2,
×4=2,
∴BE=PE+PB=2+2=4,
在Rt△ABE中,AB=![]()
∴正方形的边长为![]() .
.


科目:初中数学 来源: 题型:
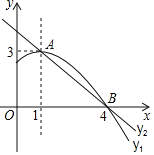
【题目】如图是抛物线![]() 图象的一部分,顶点
图象的一部分,顶点![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,下列结论:
两点,下列结论:
①![]() ;
;
②![]() ;
;
③当![]() 时,有
时,有![]() ;
;
④方程![]() 有两个相等的实数根;
有两个相等的实数根;
⑤代数式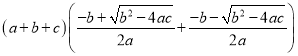 的值是6.
的值是6.
其中正确的序号有( )
A.①③④B.②④C.③⑤D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
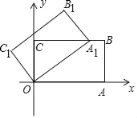
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中两条直线OC⊥BC,垂足为C,其OC=2cm,∠COB=60°,反比例函数y=![]() 的图象过点C.
的图象过点C.
(1)求:反比例函数表达式和点B的坐标.
(2)若现有长为1cm的线段MN在线段OB上沿OB方向以1cm/s的速度向点B运动(运动前点M与点O重合,N到点B停止运动),过M、N作OB的垂线分别交直线OC、BC于P、Q两点,线段MN运动的时间为ts.
①若△OMP的面积为S.求出当0<t≤1时,S与t的函数关系式.
②线段MN运动过程中,四边形MNQP有可能成为矩形吗?若可能,直接写出此时t的值;若不可能,说明理由.
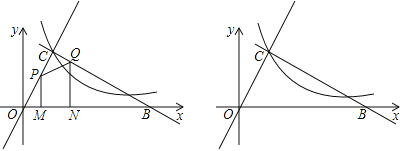
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若某抛物线上有两点A、B关于原点对称,则称该抛物线为“完美抛物线”.已知二次函数y=ax2-2mx+c(a,m,c均为常数且ac≠0)是“完美抛物线”:
(1)试判断ac的符号;
(2)若c=-1,该二次函数图象与y轴交于点C,且S△ABC=1.
①求a的值;
②当该二次函数图象与端点为M(-1,1)、N(3,4)的线段有且只有一个交点时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为

A. ![]() B. 5C. 3D.
B. 5C. 3D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
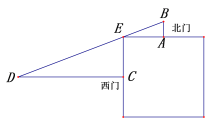
【题目】我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?” .其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B出有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,求正方形城池的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(m+1)x2﹣(m+3)x+2=0.
(1)证明:当m≠﹣1时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com