
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据三角形的内角和定理得出∠A+∠B+∠C=180°,再根据已知的条件逐个求出∠C的度数,即可得出答案.
解答 解:①∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,∴①正确;
②∵∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠C=$\frac{3}{1+2+3}$×180°=90°,
∴△ABC是直角三角形,∴②正确;
③∵∠A=90°-∠B,
∴∠A+∠B=90°,
∵∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,∴③正确;
④∵∠A=∠B=$\frac{1}{2}$∠C,
∴∠C=2∠A=2∠B,
∵∠A+∠B+∠C=180°,
∴∠A+∠A+2∠A=180°,
∴∠A=45°,
∴∠C=90°,
∴△ABC是直角三角形,∴④正确;
故选D.
点评 本题考查了三角形内角和定理的应用,能求出每种情况的∠C的度数是解此题的关键,题目比较好,难度适中.


科目:初中数学 来源: 题型:解答题
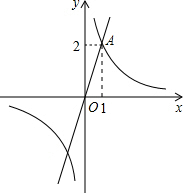 如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.
如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李叔叔刚分到一套新房,其结构如图所示(单位:m),他打算除卧室外,其余部分铺地砖.
李叔叔刚分到一套新房,其结构如图所示(单位:m),他打算除卧室外,其余部分铺地砖. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
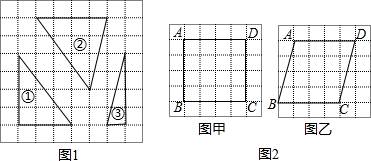
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com