
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
①将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;
②将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;
③直接写出点B2 , C2的坐标.
【答案】解:如图,△A1B1C1 , △AB2C2即为所求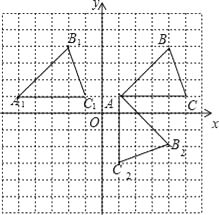
点B2(4,﹣2),C2(1,﹣3)
【解析】①利用点平移的规律写出点A、B、C的对应点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
②利用网格特点和旋转的性质画出点B、C的对应点B2、C2 , 从而得到△AB2C2;
③再写出点B2、C2的坐标。
【考点精析】本题主要考查了平移的性质和旋转的性质的相关知识点,需要掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1 . 
(1)在图中画出△A1B1C1;
(2)点A1 , B1 , C1的坐标分别为、、;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,连接MC,将菱形ABCD翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为 . 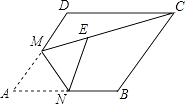
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】又到了一年中的春游季节.某班学生利用周末去参观“三军会师纪念塔”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.6m;
乙:我们相距36m.
请你根据两位同学的对话,计算纪念塔的高度.(精确到1米)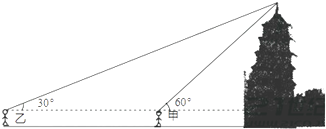
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期我们学习了一元一次方程的解法,下面是小亮同学的解题过程:
解方程:![]()
解:方程两边同时乘以15,去分母,得3(20x﹣3)﹣5(10x+4)=15……①
去括号,得60x﹣9﹣50x+20=15……②
移项,得60x﹣50x=15+9﹣20……③
合并同类项,得10x=4……④
系数化1,得x=0.4……⑤
所以x=0.4原方程的解
(1)上述小亮的解题过程从第 (填序号)步开始出现错误,错误的原因是 .
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条高铁线A,B,C三个车站的位置如图所示.已知B,C两站之间相距530千米.高铁列车从B站出发,向C站方向匀速行驶,经过13分钟距A站165千米;经过80分钟距A站500千米.
![]()
(1)求高铁列车的速度和AB两站之间的距离.(2)如果高铁列车从A站出发,开出多久可以到达C站?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:

(1)如图1,将长方形纸片ABFE沿着线段DC折叠,CF交AD于点H,过点H作HG∥DC,交线段CB于点G.
①判断∠FHG与∠EDC是否相等,并说明理由;
②说明HG平分∠AHC的理由.
(2)如图2,如果将(1)中的已知条件改为折叠三角形纸片ABE,其它条件不变.HG是否平分∠AHC?如果平分请说明理由;如果不平分,请找出∠CHG,∠AHG与∠E的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根.
(2)是否存在实数k使方程两根的倒数和为2?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com