
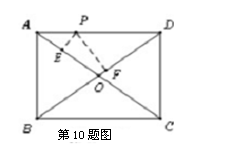
科目:初中数学 来源:不详 题型:解答题
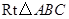 中,
中, ,
, ,
, 两点分别在
两点分别在 上,
上, ,
,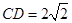 ,将
,将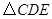 绕点
绕点 顺时针旋转,得到
顺时针旋转,得到 (如图4,点
(如图4,点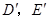 分别与
分别与 对应),点
对应),点 在
在 上,
上, 与
与 相交于点
相交于点 .
.
 的度数;
的度数; 是梯形;
是梯形; 的面积.
的面积.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 的正方形纸片和
的正方形纸片和 的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次)在下面的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),使拼出的矩形面积为a2+3ab+2b2,并标出此矩形的长和宽.
的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次)在下面的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),使拼出的矩形面积为a2+3ab+2b2,并标出此矩形的长和宽.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
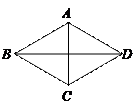
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
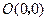 ,
,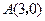 ,
,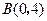 ,请你画出
,请你画出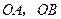 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形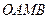 ;
; |
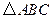 绕顶点
绕顶点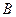 按顺时针方向旋转
按顺时针方向旋转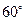 ,得到
,得到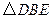 ,连结
,连结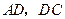 ,
,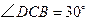 .求证:
.求证: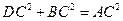 ,即四边形
,即四边形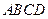 是勾股四边形
是勾股四边形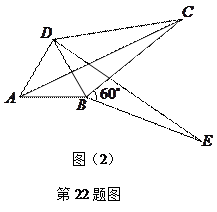
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com