
【题目】已知如图,圆P经过点A(﹣4,0),点B(6,0),交y轴于点C,∠ACB=45°,连结AP、BP. 
(1)求圆P的半径;
(2)求OC长;
(3)在圆P上是否存在点D,使△BCD的面积等于△ABC的面积?若存在求出点D坐标;若不存在说明理由.
【答案】
(1)解:∵A(﹣4,0),B(6,0)
∴AB=10,
∵∠ACB=45°,
∴∠APB=90°,
∴△PAB为等腰直角三角形,且PA=PB,
∴PA2+PB2=AB2,
解得PA=PB= ![]() ,
,
∴圆P的半径为 ![]()
(2)解:作PM⊥x轴于M,PN⊥y轴于N,连接PC,

∵△PAB为等腰直角三角形,
∴PM=AM=BM ![]() AB=5,
AB=5,
∴OM=AM﹣AO=1,
∴ON=PM=5,PN=OM=1,
在Rt△PNC中有:CN= ![]() =
= ![]() =7,
=7,
∴OC=ON+NC=5+7=12,
∴OC=12
(3)解:∵S△BCD=S△ABC,D为圆P上一点,
①当D与A重合时,仍满足条件,
∴D1(﹣4,0),
②当D与A不重合时,过A作BC的平行线,
与圆P的交点,即为所求的点D,
∵AD∥BC
∴S△BCD=S△ABC(等底等高),
作AG⊥BC于G,作DH⊥BC于H,DQ⊥x轴于Q,

∵cos∠ABC= ![]() ,sin∠ABC=
,sin∠ABC= ![]() ,
,
∴AG=ABcos∠ABC= ![]() ,
,
∵DH=AG=ABsin∠ABC= ![]() ,
,
∵∠DBC=∠DAC=∠ACB=45°,
∴BH=DH= ![]() ,
,
∴AD=GH=BH﹣BG= ![]() ,
,
∴DQ=ADsin∠DAQ=ADsin∠ABC=4,
AQ=ADcos∠DAQ=ADcos∠ABC=2,
∴OQ=OA+AQ=6,
∴D2(﹣6,4)
综上:D点的坐标为(﹣4,0)或(﹣6,4).
【解析】(1)由∠APB=2∠ACB=90°,AB=10,△PAB为等腰直角三角形,即可求得圆P的半径;(2)作PN⊥OC,PM⊥x轴,则ON=PM= ![]() AB=5,再根据勾股定理求出CN的长度,则OC=ON+NC;(3)分两种情况,①当D与A重合时,易得D(﹣4,0),②当D与A重合时,根据等底等高的性质,过A作BC的平行线,与圆P的交点即为所求的点D.
AB=5,再根据勾股定理求出CN的长度,则OC=ON+NC;(3)分两种情况,①当D与A重合时,易得D(﹣4,0),②当D与A重合时,根据等底等高的性质,过A作BC的平行线,与圆P的交点即为所求的点D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,过B作BC⊥AB交⊙O于C,过C作⊙O的切线,交AB的延长线于点D,E为AD的中点,过E作EF//BC交DC的延长线于点F,连接AF并延长BC的延长线于点G 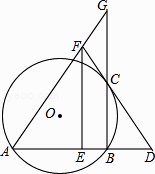
(1)求证:FC=FG;
(2)若BC=4,CG=6,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的商品市场指导价为每千克150元,公司的实际销售价格可以浮动x个百分点(即销售价格=150(1+x%)),经过市场调研发现,这种商品的日销售量p(千克)与销售价格浮动的百分点x之间的函数关系为p=﹣2x+24.若该公司按浮动﹣12个百分点的价格出售,每件商品仍可获利10%.
(1)求该公司生产销售每千克商品的成本为多少元?
(2)当该公司的商品定价为多少元时,日销售利润为576元?(说明:日销售利润=(销售价格一成本)×日销售量)
(3)该公司决定每销售一千克商品就捐赠a元利润(a≥1)给希望工程,公司通过销售记录发现,当价格浮动的百分点大于﹣1时,扣除捐赠后的日销售利润随x的增大而减小,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年6月上海语文把小学教材中“外婆”改成“姥姥一事,引起社会的广泛关注和讨论,明德集团某校文学社就此召开了一次研讨会,为了传承中国传统文化,并组织了一次全体学生“汉字听写”大赛,每位学生听写汉字39个,随机抽取了部分学生的听写结果作为样本进行整理,绘制成如下的统计图表:

组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)求统计表中的m,n,并补全条形统计图;
(2)扇形统计图中“C组“所对应的圆心角的度数是多少;
(3)已知该校共有600名学生,如果听写正确的字的个数不少于24个定为合格,请你估计该校本次听写比赛合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须既不平行也不相交(其中n是正整数)。那么当黑、白两个甲壳虫各爬行完第2017条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )

A. 0 B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图(一)、图(二)分别为甲、乙两班学生参加投篮测验的投进球数直方图.若甲、乙两班学生的投进球数的众数分别为a、b;中位数分别为c、d,则下列关于a、b、c、d的大小关系,何者正确?( ) 
A.a>b,c>d
B.a>b,c<d
C.a<b,c>d
D.a<b,c<d
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E两点分别在AC、BC上,DE为BC的中垂线,BD为∠ADE的角平分线.若∠A=58°,则∠ABD的度数为何?( ) 
A.58
B.59
C.61
D.62
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的矩形ABCD中,E为 ![]() 的中点,有一圆过C、D、E三点,且此圆分别与
的中点,有一圆过C、D、E三点,且此圆分别与 ![]() 、
、 ![]() 相交于P、Q两点.甲、乙两人想找到此圆的圆心O,其作法如下: (甲) 作∠DEC的角平分线L,作
相交于P、Q两点.甲、乙两人想找到此圆的圆心O,其作法如下: (甲) 作∠DEC的角平分线L,作 ![]() 的中垂线,交L于O点,则O即为所求;(乙) 连接
的中垂线,交L于O点,则O即为所求;(乙) 连接 ![]() 、
、 ![]() ,两线段交于一点O,则O即为所求.
,两线段交于一点O,则O即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )
A.两人皆正确
B.两人皆错误
C.甲正确,乙错误
D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com