
����Ŀ�����Ķ����в���,Ȼ�������⣮
���ϣ���������![]() ���ǵ���������
���ǵ���������![]() һ����������һ��������Ա��ཻ,�����뽻��֮����߶ΰ���������ηָ������С������,����ֵõ�����С��������һ��Ϊ����������,��һ����ԭ����������,���ǰ������߶ν�����������ε������ָ��ߣ�
һ����������һ��������Ա��ཻ,�����뽻��֮����߶ΰ���������ηָ������С������,����ֵõ�����С��������һ��Ϊ����������,��һ����ԭ����������,���ǰ������߶ν�����������ε������ָ��ߣ�
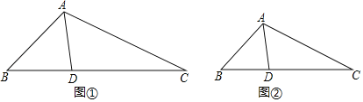
���磺��ͼ![]() ,AD��
,AD��![]() �ֳ�
�ֳ�![]() ��
��![]() ,��
,��![]() �ǵ���������,��
�ǵ���������,��![]() ��
��![]() ,��ôAD����
,��ôAD����![]() �������ָ��ߣ�
�������ָ��ߣ�
����������⣺
![]() ��ͼ
��ͼ![]() ,��
,��![]() ��,����B=40��,AD��
��,����B=40��,AD��![]() �������ָ���,��
�������ָ���,��![]() ����ADΪ�ױߵĵ���������,��
����ADΪ�ױߵĵ���������,��![]() ____�ȣ�
____�ȣ�
![]() ��
��![]() ��,��
��,��![]() ,
,![]() ,AD��
,AD��![]() �������ָ���,
�������ָ���,![]() �ǵ���������,��
�ǵ���������,��![]() ____��
____��
![]() ��ͼ
��ͼ![]() ,��
,��![]() ��,ADƽ��
��,ADƽ��![]() ,
,![]() ��֤AD��
��֤AD��![]() �������ָ��ߣ�
�������ָ��ߣ�
���𰸡���1��40����2��AB�ij�ֻ����3����3��������.
��������
��1�����������ָ������������ε����ʼ�����⣻
��2������![]() ��
��![]() ,�õ�
,�õ�![]() ���
���![]() ,�����BD���ٷ�����������ۼ�����⣻
,�����BD���ٷ�����������ۼ�����⣻
��3���������������ε��ж����������������ε����ʼ������.
![]() ��
��![]() �������ָ���,��
�������ָ���,��![]() ����ADΪ�ױߵĵ���������,
����ADΪ�ױߵĵ���������,
![]() ��
��![]() ,
,
![]() =40����
=40����
�ʴ�Ϊ40��
![]() ��
��![]() �������ָ���,
�������ָ���,![]() �ǵ���������,
�ǵ���������,
![]() ��
��![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
�ڵ���![]() ��,
��,
![]() ��
��![]() ʱ,
ʱ,![]() ��
��
![]() ��
��![]() ʱ,
ʱ,![]() ������,���������������
������,���������������
![]() ��
��![]() ʱ,
ʱ,![]() ��
��![]() ,���������������
,���������������
���AB�ij�ֻ����3��
�ʴ�Ϊ3��
![]() ֤����
֤����![]() ,
,
![]() ,
,
![]() ,
,
![]() ��
��![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() �ǵ���������,
�ǵ���������,
![]() ����
����![]() �������ָ��ߣ�
�������ָ��ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������е�ÿ��С�����εı߳�����1��ÿ��С�����εĶ�������������ABC����������A��B��C���ڸ����������ABC�Ƶ�A��˳ʱ�뷽����ת90��õ���AB��C����
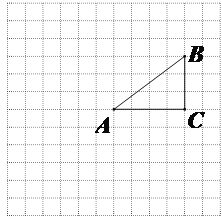
��1���������������У�������AB��C�䣻
��2�������߶�AB�ڱ任��AB��Ĺ�����ɨ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�Ƶ�A��ʱ����ת30����������AB'C'D'����B'C'��CD�ڵ�E����������ABCD�ı߳�Ϊ3����DE�ij�Ϊ_____��
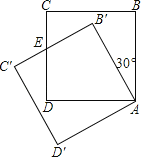
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����PD����O�ڵ�C����AB���ӳ����ڵ�D������D=2��CAD��
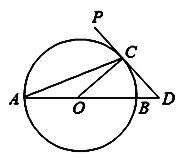
��1������D�Ķ�����
��2����CD=2����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ı���ABCD�DZ߳�Ϊ1�������Σ��ı���EFGH�DZ߳�Ϊ2�������Σ���D���F�غϣ���B��D��F����H��ͬһ��ֱ����.��������ABCD��F��H����ƽ�Ƶ���B���H�غ�ʱֹͣ.���D��F֮��ľ���Ϊx��������ABCD��������EFGH�ص����ֵ����Ϊy�����ܴ��·�ӳy��x֮�亯����ϵ��ͼ���ǣ� ��.


A. 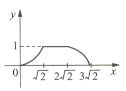 B.
B. 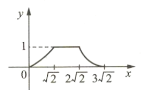 C.
C. 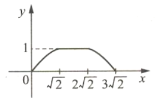 D.
D. 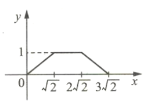
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬 AD�����C��ֱ���ഹֱ������Ϊ��D��AD����O�ڵ�E��ACƽ�֡�DAB������CE��CB��
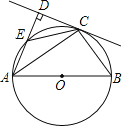
��1����֤��CD�ǡ�O�����ߣ�
��2����AC��![]() ��CE��
��CE��![]() �����O�İ뾶����
�����O�İ뾶����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC��ֱ�Ƕ���C˳ʱ����ת90�㣬�õ���A1B1C������AA1������AA1B1��15�㣬���B�Ķ������� ��

A. 75�� B. 60�� C. 50�� D. 45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
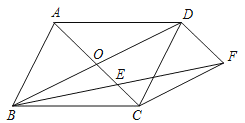
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD���ڵ�O���ֱ����C��D��CF��BD��DF��AC������BF��AC�ڵ�E��
��1����֤����FCE�ա�BOE��
��2������ADC����ʲô����ʱ���ı���OCFDΪ���Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
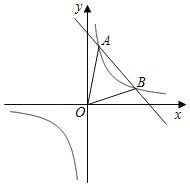
����Ŀ����ͼ��һ�κ���y1����x+5�뷴��������y2��![]() ��ͼ����A(1��m)��B(4��n)���㣮
��ͼ����A(1��m)��B(4��n)���㣮
(1)��A��B���������ͷ����������Ľ���ʽ��
(2)���AOB�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com