
【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,分别过点C、D作CF∥BD,DF∥AC,连接BF交AC于点E.
(1)求证:△FCE≌△BOE;
(2)当△ADC满足什么条件时,四边形OCFD为菱形?请说明理由.
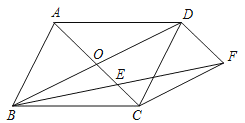
【答案】(1)见解析;(2)当△ADC满足∠ADC=90°时,四边形OCFD为菱形;理由见解析.
【解析】
(1)证明四边形OCFD是平行四边形,得出OD=CF,证出OB=CF,即可得出△FCE≌△BOE(AAS);
(2)证出四边形ABCD是矩形,由矩形的性质得出OC=OD,即可得出四边形OCFD为菱形.
(1)证明:∵CF∥BD,DF∥AC,
∴四边形OCFD是平行四边形,∠OBE=∠CFE,
∴OD=CF,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OB=CF,在
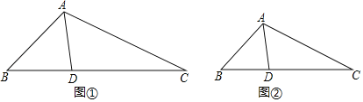
△FCE和△BOE中, ,
,
∴△FCE≌△BOE(AAS);
(2)解:当△ADC满足∠ADC=90°时,四边形OCFD为菱形;理由如下:
∵∠ADC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OC=OD,
∴四边形OCFD为菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】国贸商店服装柜在销售中发现:“宝乐牌”童装平均每天可以售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经调查发现:每件童装每降价1元,商场平均每天可多销售2件.
(1)若每件童装降价5元,则商场盈利多少元?
(2)若商场每天要想盈利1200元,请你帮助商场算一算,每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解答问题.
材料:从三角形![]() 不是等腰三角形
不是等腰三角形![]() 一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
例如:如图![]() ,AD把
,AD把![]() 分成
分成![]() 与
与![]() ,若
,若![]() 是等腰三角形,且
是等腰三角形,且![]() ∽
∽![]() ,那么AD就是
,那么AD就是![]() 的完美分割线.
的完美分割线.
解答下列问题:
![]() 如图
如图![]() ,在
,在![]() 中,若∠B=40°,AD是
中,若∠B=40°,AD是![]() 的完美分割线,且
的完美分割线,且![]() 是以AD为底边的等腰三角形,则
是以AD为底边的等腰三角形,则![]() ____度;
____度;
![]() 在
在![]() 中,若
中,若![]() ,
,![]() ,AD是
,AD是![]() 的完美分割线,
的完美分割线,![]() 是等腰三角形,则
是等腰三角形,则![]() ____;
____;
![]() 如图
如图![]() ,在
,在![]() 中,AD平分
中,AD平分![]() ,
,![]() 求证AD是
求证AD是![]() 的完美分割线.
的完美分割线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k-1)x+k2=0有两个实根x1和x2
(1) 求实数k的取值范围
(2) 若方程两实根x1、x2满足x12-x22=0,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD内一点E连接BE、CE,过C作CF⊥CE与BE延长线交于点F,连接DF、DE.CE=CF=1,DE=![]() ,下列结论中:①△CBE≌△CDF;②BF⊥DF;③点D到CF的距离为2;④S四边形DECF=
,下列结论中:①△CBE≌△CDF;②BF⊥DF;③点D到CF的距离为2;④S四边形DECF=![]() +1.其中正确结论的个数是( )
+1.其中正确结论的个数是( )
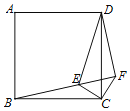
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克240元,按每千克400元出售,平均每周可售出200千克,后来经过市场调查发现,单价每降低10元,则平均每周的销售量可增加40千克,若该专卖店销售这种品牌茶叶要想平均每周获利41600元,求每千克茶叶应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
性质:在一个三角形中,各边和它所对角的正弦的比相等.
即:![]()
利用上述性质可以求解如下题目:
在![]() 中,若
中,若![]() ,
,![]() ,
,![]() ,求b.
,求b.
解:在![]() 中,∵
中,∵![]() ,
,
∴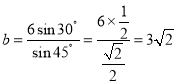 .
.
(问题解决)利用上述相关知识解决下列问题:
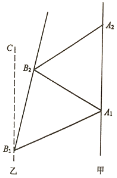
如图,甲船以每小时![]() 海里的速度向正北方向航行.当甲船位于
海里的速度向正北方向航行.当甲船位于![]() 处时,乙船位于甲船的南偏西
处时,乙船位于甲船的南偏西![]() 方向的
方向的![]() 处,且乙船从
处,且乙船从![]() 处沿北偏东
处沿北偏东![]() 方向匀速直线航行.经过20分钟后,甲船由
方向匀速直线航行.经过20分钟后,甲船由![]() 处航行到
处航行到![]() 处,乙船航行到甲船位置(即
处,乙船航行到甲船位置(即![]() 处)的南偏西
处)的南偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,求乙船每小时航行多少海里.
海里,求乙船每小时航行多少海里.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com