
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克240元,按每千克400元出售,平均每周可售出200千克,后来经过市场调查发现,单价每降低10元,则平均每周的销售量可增加40千克,若该专卖店销售这种品牌茶叶要想平均每周获利41600元,求每千克茶叶应降价多少元?
科目:初中数学 来源: 题型:
【题目】已知一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 0 | p | m | 3 |
| q | 0 | … |
(1)求这个二次函数的表达式;
(2)表格中字母m= ;(直接写出答案)
(3)在给定的直角坐标系中,画出这个二次函数的图象;
(4)以上二次函数的图象与x轴围成的封闭区域内(不包括边界),横、纵坐标都是整数的点共有 个.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点, AD与过点C的直线互相垂直,垂足为点D,AD交⊙O于点E,AC平分∠DAB,连接CE,CB.
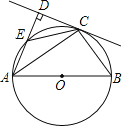
(1)求证:CD是⊙O的切线;
(2)若AC=![]() ,CE=
,CE=![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
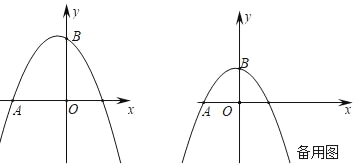
【题目】已知抛物线y=ax2﹣![]() x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
(1)求抛物线的解析式;
(2)当BQ=![]() AP时,求t的值;
AP时,求t的值;
(3)随着点P,Q的运动,抛物线上是否存在点M,使△MPQ为等边三角形?若存在,请求出t的值及相应点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
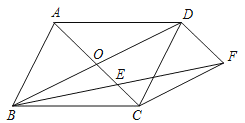
【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,分别过点C、D作CF∥BD,DF∥AC,连接BF交AC于点E.
(1)求证:△FCE≌△BOE;
(2)当△ADC满足什么条件时,四边形OCFD为菱形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
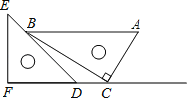
【题目】三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
如:P(1,4)的“2属派生点为P′(1+2×4,2×1+4),即P′(9,6);
(1)点P(-1,3)的“2属派生点”P′的坐标为______;
(2)若点P的“3属派生点”P′的坐标为(-1,3),则点P的坐标为______.
(3)若点P在x轴的正半轴上,点P的“k属派生点”为点P′,线段PP′的长度等于线段OP的长度,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com