
【题目】阅读材料,回答问题
一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20![]() 海里的圆形区域(包括边界)都属台风区,当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB = 100海里.
海里的圆形区域(包括边界)都属台风区,当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB = 100海里.
(1) 若这艘轮船自A处按原速度和方向继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,说明理由;
(2) 现轮船自A处立即提高船速,向位于北偏东60方向,相距60海里的D港驶去,为使台风到来之前,到达D港,问船速至少应提高多少(提高的船速取整数,![]() ) ?
) ?

【答案】(1)会遇到台风,最初遇到台风的时间为1小时;(2)6海里/时
【解析】试题分析:(1)设t时刻,轮船行驶到C点,台风中心运动到E点,列出轮船到台风中心的计算公式,求出即可,
(2)根据题意作出图形,再根据勾股定理可以得出此得出所用的时间,由AD的距离,则可以得出速度.
解:(1) 设途中会遇到台风.且最初遇到台风的时间为t小时,此时,轮船位于C处,台风中心移到E处,连结CE,则有AC = 20t,AE = AB-BE = 100-40t,EC = 20![]() ,
,
在Rt△AEC中,AC2 + AE2 = EC2,
∴(20t)2 + (100-40t)2 = (20![]() )2,
)2,
整理,得 t2-4t + 3 = 0,
解得 t1 = 1,t2 = 3.
所以,途中将遇到台风,最初遇到台风的时间为1小时.
(2) 设台风抵达D港的时间为t小时,此时台风中心至M点.过D作DF⊥AB,垂足为F,连结DM,

在Rt△ADF中,AD = 60,∠FAD = 60,
∴ DF = 30![]() ,FA = 30.
,FA = 30.
又 FM = FA + AB-BM = 130-40t,MD = 20![]() ,
,
∴ (30![]() )2 + (130-40t)2 = (20
)2 + (130-40t)2 = (20![]() )2,
)2,
整理,得 4t2-26t + 39 = 0,
解得 t1 =![]() ,t2 =
,t2 =![]() .
.
所以台风抵达D港时间为![]() 小时.
小时.
因轮船从A处用![]() 小时到达D港,其速度为60÷
小时到达D港,其速度为60÷![]() ≈25.5,故为使台风抵达D港之前轮船到达D港,轮船至少应提速6海里/时.
≈25.5,故为使台风抵达D港之前轮船到达D港,轮船至少应提速6海里/时.


科目:初中数学 来源: 题型:
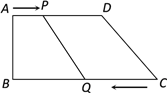
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B = 90,AD = 24厘米,AB = 8厘米,BC = 30厘米,动点P从A开始沿AD边向D以每秒1厘米的速度运动,动点Q从点C开始沿CB边向B以每秒3厘米的速度运动,P,Q分别从点A、C同时出发,当其中一点到达端点时, 另一点也随之停止运动.
设运动时间为t秒.
(1) 当t在什么时间范围时,CQ>PD?
(2) 存在某一时刻t,使四边形APQB是正
方形吗?若存在,求出t值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.无限小数都是无理数
B.若a>b,则c﹣a>c﹣b
C.立方根等于本身的数是0和1
D.平面内如果两条直线都和第三条直线垂直,那么这两条直线互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查适合抽样调查的是( )
A.改一位学生作文中的错别字
B.对班级的卫生死角进行调查
C.对八名同学的身高情况进行调查
D.对电视剧《人民的名义》收视率进行调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=120 ![]() ,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
A.1.5cm
B.2cm
C.2.5cm
D.3cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com