
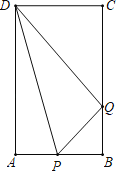
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2cm的速度移动,如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:

(1)当运动开始后1秒时,求△DPQ的面积;
(2)当运动开始后![]() 秒时,试判断△DPQ的形状;
秒时,试判断△DPQ的形状;
(3)在运动过程中,存在这样的时刻,使△DPQ以PD为底的等腰三角形,求出运动时间.
【答案】(1)S△DPQ=30(cm2);(2)△DPQ为直角三角形;(3)运动开始后第6![]() ﹣18秒时,△DPQ是以PD为底的等腰三角形.
﹣18秒时,△DPQ是以PD为底的等腰三角形.
【解析】
(1)根据运动时间求出AP,BQ,利用分割法求△DPQ的面积即可.
(2)分别求出DP2,PQ2,DQ2,进而得到PQ2+DQ2=DP2,得出答案;
(3)假设运动开始后第x秒时,满足条件,则有QP=QD,表示出QP2,QD2,列出等式,构建方程方程,求出方程的解,根据时间大于0秒小于6秒,即可解答.
解:(1)经过1秒时,AP=1,BQ=2,
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,AB=CD=6cm,BC=AD=12cm,
∴PB=6﹣1=5(cm),CQ=BC﹣BQ=12﹣2=10(cm),
∴S△DPQ=S矩形ABCD﹣S△ADP﹣S△PBQ﹣S△DCQ=72﹣![]() ×1×12﹣
×1×12﹣![]() ×6×2﹣
×6×2﹣![]() ×6×10=30(cm2).
×6×10=30(cm2).
(2)当t=![]() 秒时,
秒时,
AP=![]() ,BP=6﹣
,BP=6﹣![]() =
=![]() ,BQ=
,BQ=![]() ×2=3,CQ=12﹣3=9,
×2=3,CQ=12﹣3=9,
∴在Rt△DAP中,DP2=DA2+AP2=122+(![]() )2=
)2=![]() ,
,
在Rt△DCQ中,DQ2=DC2+CQ2=62+92=117,
在Rt△QBP中,QP2=QB2+BP2=32+(![]() )2=
)2=![]() ,
,
∴DQ2+QP2=117+![]() =
=![]() ,
,
∴DQ2+QP2=DP2,
∴△DPQ为直角三角形;
(3)假设运动开始后第x秒时,满足条件,则:QP=QD,
∵QP2=PB2+BQ2=(6﹣x)2+(2x)2,
QD2=QC2+CD2=(12﹣2x)2+62,
∴(12﹣2x)2+62=(6﹣x)2+(2x)2,
整理,得:x2+36x﹣144=0,
解得:x=﹣18±6![]() ,
,
∵0<6![]() ﹣18<6,
﹣18<6,
∴运动开始后第6![]() ﹣18秒时,△DPQ是以PD为底的等腰三角形.
﹣18秒时,△DPQ是以PD为底的等腰三角形.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
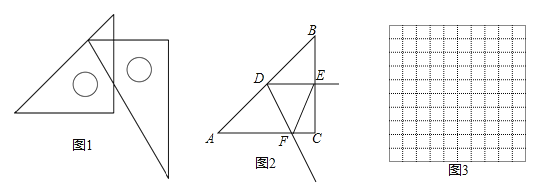
【题目】在数学活动课上,老师提出了一个问题:把一副三角尺如图摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?
小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.
下面是小林的探究过程,请补充完整:
(1)画出几何图形,明确条件和探究对象;
如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=60°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
(说明:补全表格时相关数据保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:

请你根据统计图回答下列问题:
(1)喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;
(2)请你估计全校500名学生中最喜欢“排球”项目的有多少名?
(3)在扇形统计图中,“篮球”部分所对应的圆心角是多少度?
(4)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
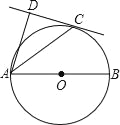
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)若CD=4,AD=8,试求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连接AC,过点D作DE⊥AC,垂足为 E.
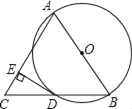
(1)求证:DC=BD;
(2)求证:DE为⊙O的切线;
(3)若AB=12,AD=6![]() ,连接OD,求扇形BOD的面积.
,连接OD,求扇形BOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
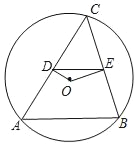
【题目】如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.
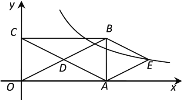
(1)求证:四边形AEBD是菱形;
(2)如果OA=4,OC=2,求出经过点E的反比例函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房成交价由今年9月份的14000元/m2下降到11月份的12600元/m2.
(1)问10、11两月平均每月降价的百分率是多少?(参考数据:![]() 0.95)
0.95)
(2)如果房价继续回落,按此降价的百分率,你预测到12月份该市的商品房成交均价是否会跌破12000元/m2?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com