
【题目】如图,直线![]() 和反比例函数
和反比例函数![]() 的图象都经过点
的图象都经过点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图象上,连接
的图象上,连接![]() .
.
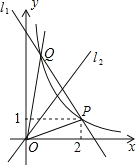
(1)求直线![]() 和反比例函数的解析式;
和反比例函数的解析式;
(2)直线![]() 经过点
经过点![]() 吗?请说明理由;
吗?请说明理由;
(3)当直线![]() 与反比例数
与反比例数![]() 图象的交点在
图象的交点在![]() 两点之间.且将
两点之间.且将![]() 分成的两个三角形面积之比为
分成的两个三角形面积之比为![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 经过点
经过点![]() ,理由见解析;(3)
,理由见解析;(3)![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
(1)依据直线l1:y=-2x+b和反比例数![]() 的图象都经过点P(2,1),可得b=5,m=2,进而得出直线l1和反比例函数的表达式;
的图象都经过点P(2,1),可得b=5,m=2,进而得出直线l1和反比例函数的表达式;
(2)先根据反比例函数解析式求得点Q的坐标为![]() ,依据当
,依据当![]() 时,y=-2×
时,y=-2×![]() +5=4,可得直线l1经过点Q;
+5=4,可得直线l1经过点Q;
(3)根据OM将![]() 分成的两个三角形面积之比为
分成的两个三角形面积之比为![]() ,分以下两种情况:①△OMQ的面积:△OMP的面积=1:2,此时有QM:PM=1:2;②OMQ的面积:△OMP的面积=2:1,此时有QM:PM=2:1,再过M,Q分别作x轴,y轴的垂线,设点M的坐标为(a,b),根据平行线分线段成比例列方程求解得出点M的坐标,从而求出k的值.
,分以下两种情况:①△OMQ的面积:△OMP的面积=1:2,此时有QM:PM=1:2;②OMQ的面积:△OMP的面积=2:1,此时有QM:PM=2:1,再过M,Q分别作x轴,y轴的垂线,设点M的坐标为(a,b),根据平行线分线段成比例列方程求解得出点M的坐标,从而求出k的值.
解:(1)∵![]() 直线和反比例函数
直线和反比例函数![]() 的图象都经过点
的图象都经过点![]() ,
,
![]() .
.
![]()
∴直线l1的解析式为y=-2x+5,反比例函数大家解析式为![]() ;
;
(2)直线![]() 经过点
经过点![]() ,理由如下.
,理由如下.![]() 点
点![]() 在反比例函数的图象上,
在反比例函数的图象上,
![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 当
当![]() 时,
时,![]() .
.
![]() 直线
直线![]() 经过点
经过点![]() ;
;
(3)![]() 的值为
的值为![]() 或
或![]() .理由如下:
.理由如下:
OM将![]() 分成的两个三角形面积之比为
分成的两个三角形面积之比为![]() ,分以下两种情况:
,分以下两种情况:
①△OMQ的面积:△OMP的面积=1:2,此时有QM:PM=1:2,
如图,过点M作ME⊥x轴交PC于点E,MF⊥y轴于点F;过点Q作QA⊥x轴交PC于点A,作QB⊥y轴于点B,交FM于点G,设点M的坐标为(a,b),
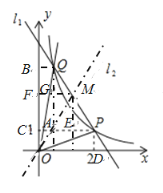
图①
∵点P的坐标为(2,1),点Q的坐标为(![]() ,4),
,4),
∴AE=a-![]() ,PE=2-a,
,PE=2-a,
∵ME∥BC,QM:PM=1:2,
∴AE:PE=1:2,
∴2-a=2(a-![]() ),解得a=1,
),解得a=1,
同理根据FM∥AP,根据QG:AG=QM:PM=1:2,
可得(4-b):(b-1)=1:2,解得b=3.
所以点M的坐标为(1,3),代入y=kx可得k=3;
②OMQ的面积:△OMP的面积=2:1,此时有QM:PM=2:1,如图②,

图②
同理可得点M的坐标为(![]() ,2),代入y=kx可得k=
,2),代入y=kx可得k=![]() .
.
故k的值为3或![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】今年本市蜜桔大丰收,某水果商销售一种蜜桔,成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量![]() (千克)与销售价
(千克)与销售价![]() (元/千克)之间的函数关系如图所示:
(元/千克)之间的函数关系如图所示:
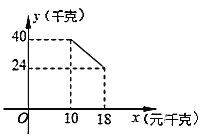
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节那天,小贤回家看到桌上有一盘粽子,其中有豆沙粽、肉粽各1个,蜜枣粽2个,这些粽子除馅外无其他差别.
(1)小贤随机地从盘中取出一个粽子,取出的是肉粽的概率是多少?
(2)小贤随机地从盘中取出两个粽子,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出蜜枣粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠COB=120°;③OA平分∠FOE;④OF=OA+OB.其中正确的有_____.
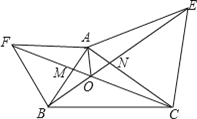
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是胡老师画的一幅写生画,四位同学对这幅画的作画时间作了猜测. 根据胡老师给出的方向坐标,猜测比较合理的是 ( )
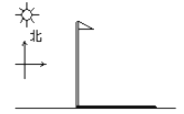
A.小明:“早上8点”B.小亮:“中午12点”
C.小刚:“下午5点”D.小红:“什么时间都行”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
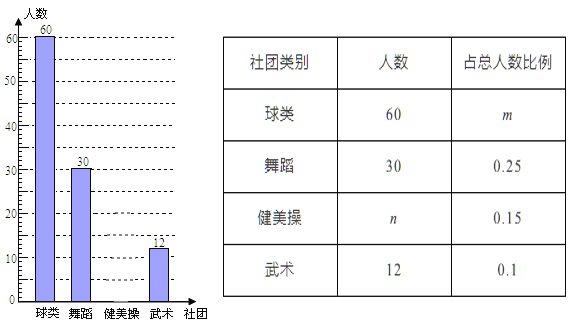
(1)求样本容量及表格中![]() 、
、![]() 的值;
的值;
(2)请补全统计图;
(3)被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3000名学生,请估计该校最喜欢足球的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国防教育和素质拓展期间,某天小明和小亮分别从校园某条路的A,B两端同时相向出发,当小明和小亮第一次相遇时,小明觉得自己的速度太慢便决定提速至原速的![]() 倍,当他到达B端后原地休息,小亮匀速到达A端后,立即按照原速返回B端(忽略掉头时间).两人相距的路程y(米)与小亮出发时间t(秒)之间的关系如图所示,当小明到达B端后,经过_____秒,小亮回到B端.
倍,当他到达B端后原地休息,小亮匀速到达A端后,立即按照原速返回B端(忽略掉头时间).两人相距的路程y(米)与小亮出发时间t(秒)之间的关系如图所示,当小明到达B端后,经过_____秒,小亮回到B端.
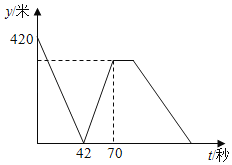
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=8,BC=10,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是______________.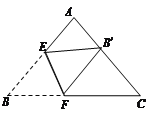
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com