
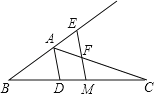
【题目】(8分)如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.
(1)求证:AE=AF;
(2)求证:BE=![]() (AB+AC).
(AB+AC).
【答案】(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)根据角平分线的性质及平行线的性质易∠AEF=∠AFE,即可得AE=AF;(2)作CG∥EM,交BA的延长线于G,已知AC=AG,根据三角形中位线定理的推论证明BE=EG,再利用三角形的中位线定理即可证得结论.
试题解析:
(1)∵DA平分∠BAC,
∴∠BAD=∠CAD,
∵AD∥EM,
∴∠BAD=∠AEF,∠CAD=∠AFE,
∴∠AEF=∠AFE,
∴AE=AF.
(2)作CG∥EM,交BA的延长线于G.
∵EF∥CG,
∴∠G=∠AEF,∠ACG=∠AFE,
∵∠AEF=∠AFE,
∴∠G=∠ACG,
∴AG=AC,
∵BM=CM.EM∥CG,
∴BE=EG,
∴BE=![]() BG=
BG=![]() (BA+AG)=
(BA+AG)=![]() (AB+AC).
(AB+AC).


科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程 x2+8x+7=0,则方程可变形为( )
A. (x-4)2=9B. (x+4)2=9C. (x-8)2=9D. (x+8)2=9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C的大小为( ) 
A.50°
B.40°
C.20°
D.25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校学生会组织学生到距学校6千米的敬老院打扫卫生,如图所示,11、12分别表示步行和骑车同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,求在距学校多远处骑车的同学追上步行的同学,此时步行的同学走了多少分钟? 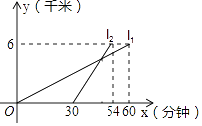
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于x,y定义一种新运算“*”:x*y=3x﹣2y,等式右边是通常的减法和乘法运算,如2*5=3×2﹣2×5=﹣4,那么(x+1)*(x﹣1)≥5的解集是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学表达式:(1)﹣3<0(2)3x+5>0(3)x2﹣6(4)x=﹣2(5)y≠0(6)x≥50中,不等式的个数是()
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com