练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在△ABC中，点D是BC上一点，∠BAD=80°，AB=AD=DC，则∠C的大小为（ ）

    A.50°
    B.40°
    C.20°
    D.25°

    【答案】D
    【解析】解：∵AB=AD，
    ∴∠B=∠ADB，
    由∠BAD=80°得∠B= =50°=∠ADB，
    ∵AD=DC，
    ∴∠C=∠ACD，
    ∴∠C= ∠ADB=25°
    故选D．
    【考点精析】根据题目的已知条件，利用三角形的内角和外角和等腰三角形的性质的相关知识可以得到问题的答案，需要掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角；等腰三角形的两个底角相等（简称：等边对等角）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】计算下列各式．
    （1）（ ﹣ ）（4 + ）﹣ ；
    （2）（a + ）÷ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解不等式组 ，并在数轴上表示出其解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

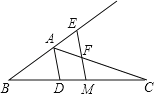
    【题目】（8分）如图，已知△ABC，AD平分∠BAC交BC于点D，BC的中点为M，ME∥AD，交BA的延长线于点E，交AC于点F．

    （1）求证：AE=AF；

    （2）求证：BE=（AB+AC）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝ax2＋bx－3与x轴交于点A（1，0）和点B，与y轴交于点C，且其对称轴l为x＝－1，点P是抛物线上B，C之间的一个动点（点P不与点B，C重合）．

    （1）直接写出抛物线的解析式；

    （2）小唐探究点P的位置时发现：当动点N在对称轴l上时，存在PB⊥NB，且PB＝NB的关系，请求出点P的坐标；

    （3）是否存在点P使得四边形PBAC的面积最大？若存在，请求出四边形PBAC面积的最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知如图，直线AB、CD相交于点O，∠COE=90°．
    （1）若∠AOC=36°，求∠BOE的度数；
    （2）若∠BOD：∠BOC=1：5，求∠AOE的度数；
    （3）在（2）的条件下，过点O作OF⊥AB，请直接写出∠EOF的度数．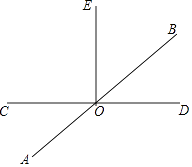

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD∥BC，∠BAD=90°，以点B为圆心，BC长为半径画弧，与射线AD相交于点E，连接BE，过C点作CF⊥BE，垂足为F．线段BF与图中现有的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明．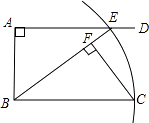

    （1）结论：BF= ．
    （2）证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明是一位善于思考的学生，在一次数学活动课上，他将一副直角三角板按如图所示的位置摆放，A、B、D三点在同一直线上，EF∥AD，∠CAB=∠EDF=90°，∠C=45°，∠E=60°，量得DE=8．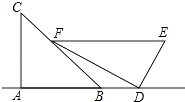

    （1）试求点F到AD的距离．
    （2）试求BD的长．

    查看答案和解析>>

    同步练习册答案