
【题目】如图,抛物线y=ax2+bx-3与x轴交于点A(1,0)和点B,与y轴交于点C,且其对称轴l为x=-1,点P是抛物线上B,C之间的一个动点(点P不与点B,C重合).
(1)直接写出抛物线的解析式;
(2)小唐探究点P的位置时发现:当动点N在对称轴l上时,存在PB⊥NB,且PB=NB的关系,请求出点P的坐标;
(3)是否存在点P使得四边形PBAC的面积最大?若存在,请求出四边形PBAC面积的最大值;若不存在,请说明理由.

【答案】 (1)抛物线的解析式为y=x2+2x-3;
(2点P的坐标为(-1-![]() ,-2);
,-2);
(3)存在,四边形PBAC的面积最大,最大值为![]() .
.
【解析】(1)由抛物线y=ax2+bx-3(a≠0)点A(1,0)和点B(-3,0),由待定系数法就可以直接求出a、b的值而求出抛物线的解析式.
(2)由(1)的解析式就可以求出C点的坐标,求出OC的值,在Rt△CON中由勾股定理就可以求出CN的值,CP1=NP1时,
作P1H⊥CN于H,由三角形相似就可以求出P1N的值,从而求出P1的坐标;
(3)设出点E的坐标,连接BE、CE,作EG⊥OB于点G,就可以表示EG、BG、OG的值就可以表示出四边形BOCE的面积,然后化为顶点式就可以求出其面积的最大值.
解:(1)抛物线的解析式为y=x2+2x-3.
(2)
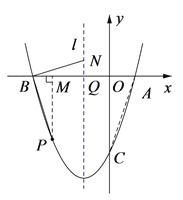
如图,过点P作PM⊥x轴于点M,
设抛物线对称轴l交x轴于点Q.
∵PB⊥NB,∴∠PBN=90°,
∴∠PBM+∠NBQ=90°.
∵∠PMB=90°,
∴∠PBM+∠BPM=90°.
∴∠BPM=∠NBQ.
又∵∠BMP=∠BNQ=90°,PB=NB,
△BPM≌△NBQ.∴PM=BQ.
∵抛物线y=x2+2x-3与x轴交于点A(1,0)和点B,且对称轴为x=-1,
∴点B的坐标为(-3,0),点Q的坐标为(-1,0).∴BQ=2.∴PM=BQ=2.
∵点P是抛物线y=x2+2x-3上B、C之间的一个动点,
∴结合图象可知点P的纵坐标为-2.
将y=-2代入y=x2+2x-3,得-2=x2+2x-3.
解得x1=-1-![]() ,x2=-1+
,x2=-1+![]() (舍去).
(舍去).
∴此时点P的坐标为(-1-![]() ,-2).
,-2).
(3)存在.
如图,连接AC.可设点P的坐标为(x,y)(-3﹤x﹤0),
则y=x2+2x-3.∵点A(1,0),∴OA=1.
∵点C是抛物线与y轴的交点,∴令x=0,得y=-3.即点C(0,-3).
∴OC=3.由(2)可知
S四边形PBAC=S△BPM+S四边形PMOC+S△AOC
=![]() BM·PM+
BM·PM+![]() (PM+OC)·OM+
(PM+OC)·OM+![]() OA·OC
OA·OC
=![]() (x+3)(-y)+
(x+3)(-y)+![]() (-y+3)(-x)+
(-y+3)(-x)+![]() ×1×3
×1×3
=-![]() y-
y-![]() x+
x+![]() .将y=x2+2x-3代入可得
.将y=x2+2x-3代入可得
S四边形PBAC=-![]() (x2+2x-3)-
(x2+2x-3)-![]() x+
x+![]()
=-![]() (x+
(x+![]() )2+
)2+![]() .∵-
.∵-![]() ﹤0,-3﹤x﹤0,
﹤0,-3﹤x﹤0,
∴当x=-![]() 时,S四边形PBAC有最大值
时,S四边形PBAC有最大值![]() .
.
此时,y=x2+2x-3=-![]() .
.
∴当点P的坐标为(-![]() ,-
,-![]() )时,
)时,
四边形PBAC的面积最大,最大值为![]() .
.
“点睛”本题考查了二次函数的综合题:熟练掌握二次函数的性质和二次函数图象上点的坐标特征;会运用待定系数法求函数的解析式;能灵活运用相似三角形性质表示线段之间的关系;理解坐标与图形性质,会运用勾股定理的逆定理证明三角形为直角三角形;学会用分类讨论的思想解决数学问题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,点D是弦AB的中点,点C在⊙O上,CD经过圆心O,则下列结论中不一定正确的是( )
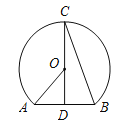
A. CD⊥AB B. ∠OAD =2∠CBD C. ∠AOD =2∠BCD D. 弧AC = 弧BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家.其中x表示时间,y表示小明离他家的距离,若小明家、超市、书店在同一条直线上.
根据图象回答下列问题: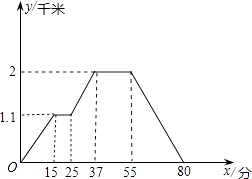
(1)超市离小明家多远,小明走到超市用了多少时间?
(2)超市离书店多远,小明在书店购书用了多少时间?
(3)书店离小明家多远,小明从书店走回家的平均速度是每分钟多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C的大小为( ) 
A.50°
B.40°
C.20°
D.25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,属于必然事件的是( )
A. 打开电视机正在播放广告B. 投掷一枚质地均匀的硬币100次,正面向上的次数为50次
C. 任意画一个三角形,其内角和为180°D. 任意一个二次函数图象与x轴有交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N. 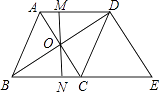
(1)请你判断OM和ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com