
【题目】小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板按如图所示的位置摆放,A、B、D三点在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8. 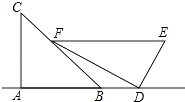
(1)试求点F到AD的距离.
(2)试求BD的长.
【答案】
(1)解:如图,过点F作FM⊥AD于点M,
在△EDF中,∠EDF=90°,∠E=60°,DE=8,
则∠DFE=30°,
故EF=2DE=16,
DF= ![]() =
= ![]() =8
=8 ![]() ,
,
∵AB∥EF,
∴∠FDM=∠DFE=30°,
在Rt△FMD中,MF= ![]() DF=8
DF=8 ![]() ×
× ![]() =4
=4 ![]() ,
,
即点F与AD之间的距离为:4 ![]()
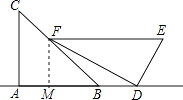
(2)解:在Rt△FMD中,DM= ![]() =
= ![]() =12,
=12,
∵∠C=45°,∠CAB=90°,
∴∠CBA=45°,
又∵∠FMB=90°,
△FMB是等腰直角三角形,
∴MB=FM=4 ![]() ,
,
∴BD=MD﹣FM=12﹣4 ![]()
【解析】(1)根据题意得出∠DFE=30°,则EF=2DE=16,进而利用勾股定理得出DF的长,进而得出答案;(2)直接利用勾股定理得出DM的长,进而得出MB=FM,求出答案.
【考点精析】根据题目的已知条件,利用平行线的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C的大小为( ) 
A.50°
B.40°
C.20°
D.25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学表达式:(1)﹣3<0(2)3x+5>0(3)x2﹣6(4)x=﹣2(5)y≠0(6)x≥50中,不等式的个数是()
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N. 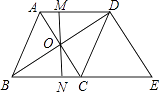
(1)请你判断OM和ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a、b被直线c所截,下列说法正确的是( ) 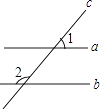
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b
查看答案和解析>>
科目:初中数学 来源: 题型:
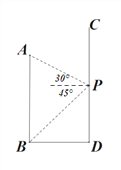
【题目】如图,AB、CD分别表示两幢相距36米的大楼,小明同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°.
(1)求PD的高;
(2)求大楼AB的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com