练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图(12)，已知∠BED=∠B+∠D，试说明AB与CD的关系。

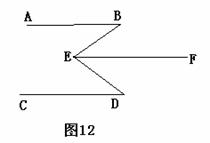     解：AB∥CD，理由如下：

      过点E作∠BEF=∠B 

    ∴AB∥EF（                      ）

     ∵∠BED=∠B+∠D

     ∴∠FED=∠D

     ∴CD∥EF（                       ）

     ∴AB∥CD（                       ）


     解：AB∥CD，理由如下：

      过点E作∠BEF=∠B 

    ∴AB∥EF（内错角相等，两直线平行）

     ∵∠BED=∠B+∠D

     ∴∠FED=∠D

     ∴CD∥EF（内错角相等，两直线平行 ）

     ∴AB∥CD（如果两条直线都与第三条直线平行，那么这两条直线也互相平行）

      


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，已知菱形ABCD的边长为4，∠A=60°，对称中心为点P，点F为BC边上一个动点，点E在AB边上，且满足条件∠EPF=60°，图中两块阴影部分图形关于直线AC成轴对称，设它们的面积和为S1．

    （1）求证：∠APE=∠CFP；

    （2）设四边形CMPF的面积为S2，CF=x，．

    ①求y关于x的函数解析式和自变量x的取值范围，并求出y的最大值；

    ②当图中两块阴影部分图形关于点P成中心对称时，求y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于x的方程x2－（m＋2）x＋（2m－1）=0的一个根是2，请求出方程的另一个根，并求以此两根为边长的直角三角形的面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图3，PO⊥OR，OQ⊥PR，则点O到PR所在直线的距离是线段的长（    ）

     A、PO     B、RO     C、OQ    D、PQ   

        

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    “两直线平行，同位角相等。”的题设是             ，结论是              。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图（17），点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA求证：∠FDE=∠A。（5分）

                                                        

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    两平行直线被第三条直线所截，同旁内角的平分线(    ) 

    A.互相重合      B.互相平行     C.互相垂直       D.无法确定 

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在如图20的方格纸上平移所给的火炬图案，使点A移到点A′的位置

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，小明从点O出发，先向西走40米，再向南走30米到达点M，如果点M的位置用(－40，－30)表示，那么(10，20)表示的位置是（    ）。

    A．点A   B．点B   　C．点C 　 　D．点D

    查看答案和解析>>

    同步练习册答案