
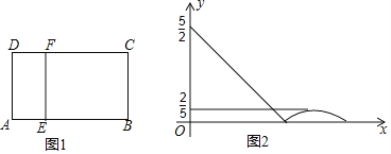
【题目】如图1,在矩形ABCD中,动点E从A出发,沿![]() 方向运动,当点E到达点C时停止运动,过点E做
方向运动,当点E到达点C时停止运动,过点E做![]() ,交CD于F点,设点E运动路程为x,
,交CD于F点,设点E运动路程为x, ![]() ,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是
,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是![]() ,则矩形ABCD的面积是( )
,则矩形ABCD的面积是( )
A. ![]() B.
B. ![]() C. 6 D. 5
C. 6 D. 5
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
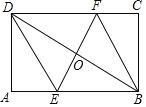
(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F在对角线BD上,且BF=DE.
⑴求证:四边形AECF是菱形.
⑵若AB=2,BF=1,求四边形AECF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
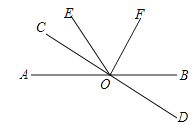
【题目】如图,直线AB和CD交于点O,∠COF=90°,OC平分∠AOE,∠COE=40°.
(1)求∠BOD的度数;
(2)OF平分∠BOE吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):
方案一:提供8000元赞助后,每张票的票价为50元;
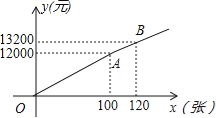
方案二:票价按图中的折线OAB所表示的函数关系确定.
(1)若购买120张票时,按方案一和方案二分别应付的购票款是多少?
(2)求方案二中y与x的函数关系式;
(3)至少买多少张票时选择方案一比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】福建省教育厅日前发布文件,从2019年开始,体育成绩将按一定的原始分计入中考总分。某校为适应新的中考要求,决定为体育组添置一批体育器材。学校准备在网上订购一批某品牌足球和跳绳,在查阅天猫网店后发现足球每个定价150元,跳绳每条定价30元.现有A、B两家网店均提供包邮服务,并提出了各自的优惠方案.
A网店:买一个足球送一条跳绳;
B网店:足球和跳绳都按定价的90%付款.
已知要购买足球40个,跳绳x条(x>40)
(1)若在A网店购买,需付款 元(用含x的代数式表示).
若在B网店购买,需付款 元(用含x的代数式表示).
(2)若x=100时,通过计算说明此时在哪家网店购买较为合算?
(3)当x=100时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,
并计算需付款多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com