
【题目】如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En,则O2016E2016=_____AC.

【答案】![]()
【解析】
由O1E1∥AC可得出△BO1E1∽△BAC和△E1O1O2∽△ACO2,由相似三角形的性质可得出![]() =
=![]() 和
和![]() =
=![]() ,结合三角形中位线定理即可得出O2E2=
,结合三角形中位线定理即可得出O2E2=![]() AC,同理即可得出OnEn=
AC,同理即可得出OnEn=![]() AC,再代入n=2016即可得出结论.
AC,再代入n=2016即可得出结论.
解:∵O1E1∥AC,
∴∠BO1E1=∠BAC,∠BE1O1=∠BCA,
∴△BO1E1∽△BAC,
∴![]() =
=![]() .
.
∵CO1是△ABC的中线,
∴![]() =
=![]() =
=![]() .
.
∵O1E1∥AC,
∴∠O1E1O2=∠CAO2,∠E1O1O2=∠ACO2,
∴△E1O1O2∽△ACO2,
∴![]() =
=![]() =
=![]() .
.
∵O2E2∥AC,
∴![]() =
=![]() =
=![]() ,
,
∴O2E2=![]() AC.
AC.
同理:OnEn=![]() AC.
AC.
∴O2016E2016=![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】下图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4.若用想x,y表示直角三角形的两直角边(x>y),则下列四个说法:①![]() ,②x-y=2,③2xy+4=49,④x+y=9其中说法正确的是( )
,②x-y=2,③2xy+4=49,④x+y=9其中说法正确的是( )

A. ①②B. ①②③④C. ②④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD.
(1)求证:BD=AE;
(2)如图2,若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
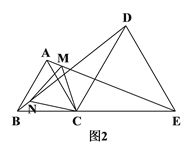
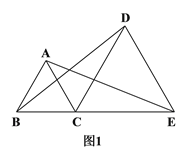
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知:点A(0,0),B(![]() ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第
,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第![]() 个等边三角形的边长等于__________.
个等边三角形的边长等于__________.
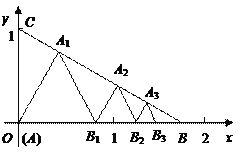
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣4)﹣m2=0.
(1)求证:对任意实数m,方程总有2个不相等的实数根;
(2)若方程的一个根是2,求m的值及方程的另一个根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com