

分析 (1)根据折叠的性质得出∠ADB=∠EDB,根据平行线的性质得出∠ADB=∠DBC,从而求得∠BDE=∠DBC,根据等角对等边得出BF=DF,即可证得△BDF为等腰三角形,设BF=DF=x,则FC=8-x,在RT△DCF中,根据勾股定理即可求得BF的长;
(2)由折叠性质得DH=BH,设BH=DH=y,则CH=8-y,在RT△CDH中,根据勾股定理求得BH、DH的长,由翻折的性质可得,BG=DG,∠BHG=∠DHG,进而得出∠DHG=∠DGH,根据等角对等边得出DH=DG,从而得出BH=DH=DG=BG,证得四边形BHDG是菱形,然后根据S菱形=$\frac{1}{2}$BD•GH=BH•CD,即可求得GH的长.
解答 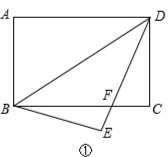 解:(1)如图①,由折叠得,∠ADB=∠EDB,AD=DE,AB=BE,
解:(1)如图①,由折叠得,∠ADB=∠EDB,AD=DE,AB=BE,
∵在矩形ABCD中,AD∥BC,
∴∠ADB=∠DBC,
∴∠BDE=∠DBC,
∴BF=DF,
∴△BDF为等腰三角形,
∵AB=6,BC=8.
∴DE=8,
设BF=DF=x,
∴FC=8-x,
在RT△DCF中,DF2=DC2+FC2,
∴x2=62+(8-x)2,解得x=$\frac{25}{4}$,
∴BF的长为$\frac{25}{4}$;
(2)如图②,由折叠得,DH=BH,设BH=DH=y,则CH=8-y,
在RT△CDH中,DH2=DC2+CH2,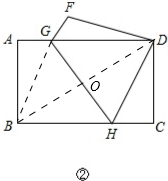
即y2=62+(8-y)2,解得y=$\frac{25}{4}$,
连接BD、BG,
由翻折的性质可得,BG=DG,∠BHG=∠DHG,
∵在矩形ABCD中,AD∥BC,
∴∠BHG=∠DGH,
∴∠DHG=∠DGH,
∴DH=DG,
∴BH=DH=DG=BG,
∴四边形BHDG是菱形,
在RT△BCD中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=10,
∵S菱形=$\frac{1}{2}$BD•GH=BH•CD,即$\frac{1}{2}$×10•GH=$\frac{25}{4}$×6,
解得GH=$\frac{15}{2}$.
点评 本题考查了折叠的性质,平行线的性质,等腰三角形的性质勾股定理的应用菱形的判定,菱形的面积等,折叠的性质的应用是本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (2,-3) | C. | (2,-1) | D. | (2,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x米,面积为y平方米.
如图,在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x米,面积为y平方米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
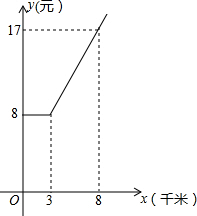 如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图,根据图象回答下列问题:
如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
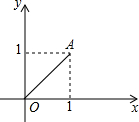 如图,点A的坐标是(1,1),如果将线段OA绕点O按逆时针方向旋转135°,那么点A旋转后的对应点的坐标是( )
如图,点A的坐标是(1,1),如果将线段OA绕点O按逆时针方向旋转135°,那么点A旋转后的对应点的坐标是( )| A. | (-$\sqrt{2}$,0) | B. | (0,-$\sqrt{2}$) | C. | (0,-1) | D. | (-1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
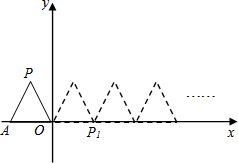 如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2013次,点P依次落在点P1,P2,P3…P2013的位置,则点P2013的横坐标为2012.5.
如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2013次,点P依次落在点P1,P2,P3…P2013的位置,则点P2013的横坐标为2012.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com