
【题目】如图:在数轴上A点表示数![]() ,B点示数
,B点示数![]() ,C点表示数
,C点表示数![]() ,
,![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() .
.
![]()
(1)![]() =__________,
=__________,![]() =__________,
=__________,![]() =__________;
=__________;
(2)若将数轴折叠,使得A点与C点重合,则点B与数__________表示的点重合;
(3)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动,假设![]() 秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求
秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求![]() 的值;
的值;
(4)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动时,小聪同学发现:当点C在B点右侧时,![]() BC+3AB的值是个定值,求此时
BC+3AB的值是个定值,求此时![]() 的值.
的值.
【答案】(1)![]() =-3,
=-3,![]() =1,
=1,![]() =9;(2)5;(3)1, 16, 4;(4)
=9;(2)5;(3)1, 16, 4;(4)![]() =1.
=1.
【解析】
试题(1)根据非负数的意义求出a、c的值,根据最小的正整数求出b;
(2)根据对称性可求解;
(3)分别以A、B、C为中点,分别求解即可;
(4)分别求出此时的BC、AB的长,然后由![]() BC+3AB可代入相应的速度值求解是定值的m.
BC+3AB可代入相应的速度值求解是定值的m.
试题解析:(1)因为b是最小的正整数,可得b=1,
根据![]() ,求得
,求得![]() =-3,
=-3,![]() =9;
=9;
(2)根据对称性可求解:(-3+9)×2=3,
3-1=2,
3+2=5
答案为:5.
(3)B为中点时,![]() ,
,
解得
![]() =1,
=1,
A为中点时,![]()
解得![]() =16,
=16,
C为中点时,![]()
解得![]() =4;
=4;
(4)由题意可知,AB=4+t,
BC=8-3t
所以m·BC+3AB
=m·(8-3t)+3(4+t)
=8m+12-(3m-3)t
由定值可知3m-3=0
解得![]() =1.
=1.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
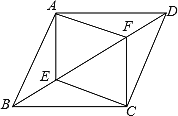
【题目】如图,在平行四边形ABCD中,E、F是对角线BD上的两点,且BE=DF.
(1)求证:AE=CF;
(2)连接AF、CE,判断四边形AECF的形状,并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
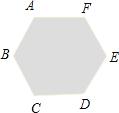
【题目】如图,在正六边形ABCDEF内放入2008个点,若这2008个点连同正六边形的六个顶点无三点共线,则该正六边形被这些点分成互不重合的三角形共_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() ,则称
,则称![]() 与
与![]() 是关于
是关于![]() 的关联数.例如:若
的关联数.例如:若![]() ,则称
,则称![]() 与
与![]() 是关于2的关联数;
是关于2的关联数;
(1)若3与![]() 是关于2的关联数,则
是关于2的关联数,则![]() _______.
_______.
(2)若![]() 与
与![]() 是关于2的关联数,求
是关于2的关联数,求![]() 的值.
的值.
(3)若![]() 与
与![]() 是关于
是关于![]() 的关联数,
的关联数, ![]() ,
,![]() 的值与
的值与![]() 无关,求
无关,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
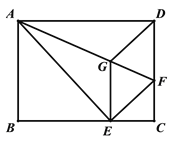
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)若AG=7、GF=3,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
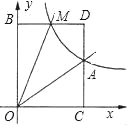
【题目】如图,已知正比例函数y=ax与反比例函数y=![]() 的图象交于点A(3,2)
的图象交于点A(3,2)
(1)求上述两函数的表达式;
(2)M(m,n)是反比例函数图象上的一个动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A点作直线AC∥y轴交x轴于点C,交直线MB于点D.若s四边形OADM=6,求点M的坐标,并判断线段BM与DM的大小关系,说明理由;
(3)探索:x轴上是否存在点P.使△OAP是等腰三角形?若存在,求出点P的坐标; 若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=(k﹣1)x+k+1和直线l2:y=kx+k+2,其中k为不小于2的自然数.
(1)当k=2时,直线l1、l2与x轴围成的三角形的面积S2=______;
(2)当k=2、3、4,……,2018时,设直线l1、l2与x轴围成的三角形的面积分别为S2,S3,S4,……,S2018,则S2+S3+S4+……+S2018=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
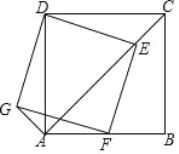
【题目】如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩 形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB中点,连接DF交AC于点M,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
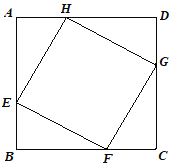
【题目】如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.则四边形EFGH面积的最小值是________cm2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com